P03: Merkle Tree Library
Project Overview
| Attribute | Value |
|---|---|
| Main Language | Go |
| Alternative Languages | Rust, C, TypeScript |
| Difficulty | Intermediate |
| Coolness Level | Level 3: Genuinely Clever |
| Business Potential | Resume Gold (Educational/Personal Brand) |
| Knowledge Area | Data Structures / Blockchain |
| Main Book | “Mastering Bitcoin” by Andreas M. Antonopoulos |
Learning Objectives
By completing this project, you will:
- Understand Merkle tree construction including handling odd numbers of leaves, tree balancing strategies, and recursive hashing patterns
- Master inclusion proof generation by identifying and collecting sibling hashes along the authentication path from leaf to root
- Implement proof verification reconstructing the root hash from a leaf and its proof to confirm membership without accessing the full dataset
- Explore sparse Merkle trees understanding how to efficiently represent mostly-empty trees for applications like state proofs
- Connect theory to practice understanding why Merkle trees are fundamental to Bitcoin’s light clients, Ethereum’s state trie, and certificate transparency logs
Deep Theoretical Foundation
The Problem: How Do You Verify Without Downloading Everything?
Imagine you want to confirm that a specific transaction is included in a Bitcoin block. The block might contain thousands of transactions. Do you need to download all of them to verify just one?
Without Merkle trees, the answer would be yes. You’d need to:
- Download all transactions
- Hash them all together
- Compare with the block header’s transaction root
This is impractical for mobile wallets, embedded devices, or any resource-constrained client. A single Bitcoin block can be several megabytes, and there are hundreds of thousands of blocks.
Merkle trees solve this with a brilliant insight: you can prove membership in O(log n) data instead of O(n).
What Is a Merkle Tree?
A Merkle tree (named after Ralph Merkle, who patented the concept in 1979) is a binary tree where:
- Leaves contain hashes of data items
- Interior nodes contain hashes of their children
- The root is a single hash summarizing all data
┌───────────────┐
│ Root Hash │
│ H(H01 || H23)│
└───────┬───────┘
│
┌─────────────┴─────────────┐
│ │
┌─────┴─────┐ ┌─────┴─────┐
│ H01 │ │ H23 │
│ H(H0||H1) │ │ H(H2||H3) │
└─────┬─────┘ └─────┬─────┘
│ │
┌───────┴───────┐ ┌───────┴───────┐
│ │ │ │
┌──┴──┐ ┌──┴──┐ ┌──┴──┐ ┌──┴──┐
│ H0 │ │ H1 │ │ H2 │ │ H3 │
│H(D0)│ │H(D1)│ │H(D2)│ │H(D3)│
└──┬──┘ └──┬──┘ └──┬──┘ └──┬──┘
│ │ │ │
┌──┴──┐ ┌──┴──┐ ┌──┴──┐ ┌──┴──┐
│ D0 │ │ D1 │ │ D2 │ │ D3 │
│Data │ │Data │ │Data │ │Data │
└─────┘ └─────┘ └─────┘ └─────┘
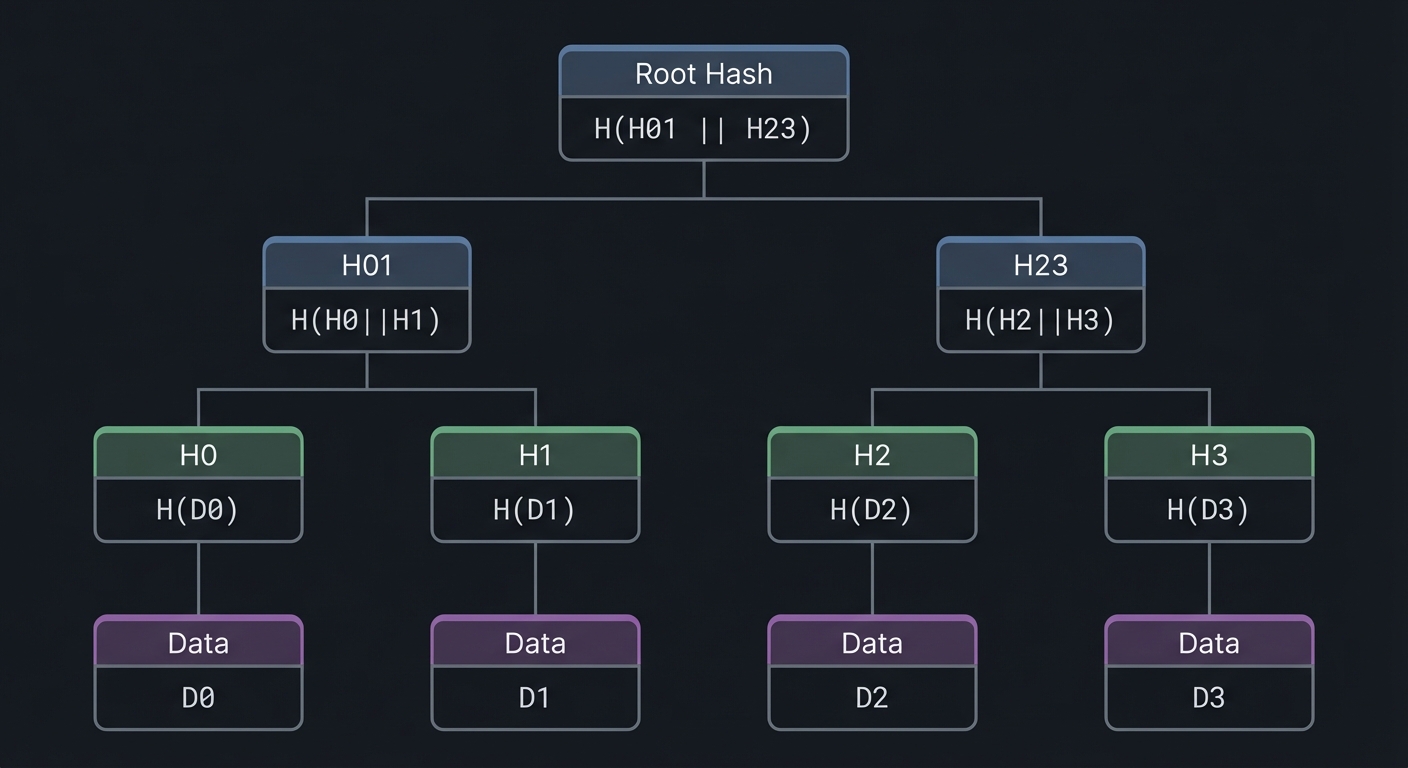
Key properties:
- Deterministic: Same data always produces the same root hash
- Tamper-evident: Any change to any leaf completely changes the root
- Efficient verification: Prove membership with O(log n) hashes
The Magic of Merkle Proofs
Suppose you have the root hash and want to verify that D2 is in the tree. You don’t need all the data—you only need the authentication path: the sibling hashes along the path from D2 to the root.
Proving D2 is in the tree:
Step 1: Hash D2 → H2
Step 2: Need H3 (sibling) → compute H23 = H(H2 || H3)
Step 3: Need H01 (sibling) → compute Root = H(H01 || H23)
Step 4: Compare computed root with known root
Proof = [H3, H01, directions]
Size = O(log n) = 2 hashes for 4 leaves
For a tree with 1 million leaves, a proof requires only ~20 hashes (log₂(1,000,000) ≈ 20), regardless of which leaf you’re proving. That’s about 640 bytes instead of downloading all 1 million items!
Why Merkle Trees Enable Light Clients
A light client (also called SPV client for “Simplified Payment Verification” in Bitcoin) is a wallet that:
- Downloads only block headers (80 bytes each in Bitcoin)
- Requests Merkle proofs for specific transactions
- Verifies inclusion without trusting the full node
This is how your mobile Bitcoin wallet works. It doesn’t download 500+ GB of blockchain—it requests proofs.
The security model:
- Light client trusts that the longest chain represents valid consensus
- Full nodes provide Merkle proofs for transactions
- Light client can verify inclusion cryptographically
- Even if a full node lies, it cannot forge a valid proof for a non-existent transaction
Handling Odd Numbers of Leaves
Real-world data rarely has a power-of-2 count. Different implementations handle odd counts differently:
Strategy 1: Duplicate the last leaf (Bitcoin style)
Leaves: [D0, D1, D2]
H(H01 || H22')
/ \
H01 H22'
/ \ / \
H0 H1 H2 H2 ← D2 is duplicated
Strategy 2: Promote the orphan (some implementations)
Leaves: [D0, D1, D2]
H(H01 || H2)
/ \
H01 H2 ← H2 promoted directly
/ \ |
H0 H1 D2
Strategy 3: Use padding (Ethereum-style)
Leaves: [D0, D1, D2, <empty>]
H(H01 || H23)
/ \
H01 H23
/ \ / \
H0 H1 H2 H_empty
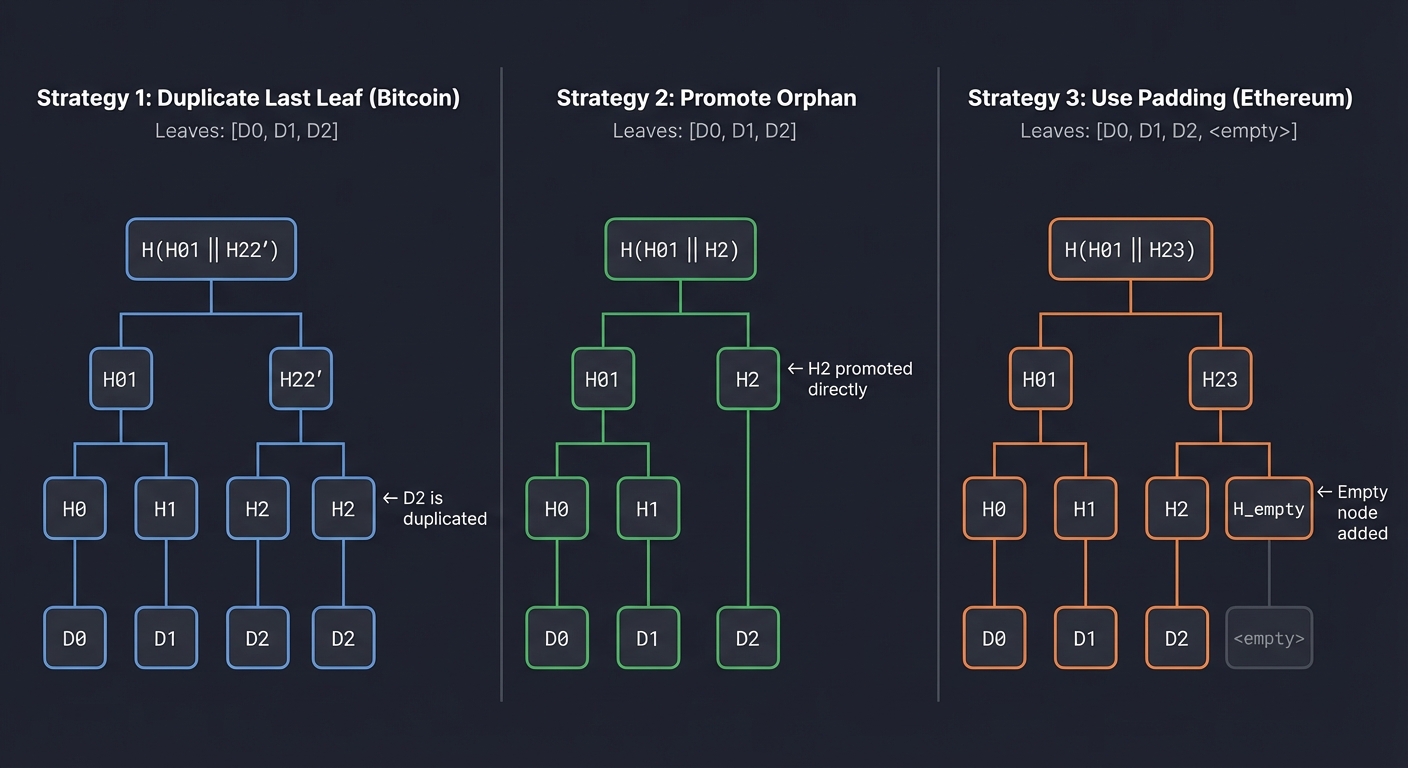
Bitcoin uses Strategy 1, which has a subtle security implication: CVE-2012-2459 was a vulnerability where duplicated leaves could be exploited. Modern implementations include defenses.
Tree Construction: The Algorithm
Building a Merkle tree is elegantly recursive:
function build_tree(data_items):
// Base case: hash the leaves
leaves = [hash(item) for item in data_items]
// Handle odd count by duplicating last element
if len(leaves) is odd:
leaves.append(leaves[-1])
return build_level(leaves)
function build_level(nodes):
// Base case: single node is the root
if len(nodes) == 1:
return nodes[0]
// Pair up nodes and hash
next_level = []
for i in range(0, len(nodes), 2):
combined = hash(nodes[i] || nodes[i+1])
next_level.append(combined)
// Handle odd count at this level
if len(next_level) > 1 and len(next_level) is odd:
next_level.append(next_level[-1])
return build_level(next_level)
Proof Generation: Collecting Siblings
To generate a proof for a leaf at index idx:
function generate_proof(tree, leaf_index):
proof = []
index = leaf_index
level = 0 // Start at leaves
while level < tree.height:
// Get sibling index
if index is even:
sibling_index = index + 1
else:
sibling_index = index - 1
// Record sibling hash and direction
sibling = tree.get_node(level, sibling_index)
is_left = (index is odd) // Sibling is on the left
proof.append((sibling, is_left))
// Move up the tree
index = index / 2
level = level + 1
return proof
Proof Verification: Reconstructing the Root
To verify a proof:
function verify_proof(leaf_hash, proof, expected_root):
current = leaf_hash
for (sibling, sibling_is_left) in proof:
if sibling_is_left:
current = hash(sibling || current)
else:
current = hash(current || sibling)
return current == expected_root
Sparse Merkle Trees: Efficient Empty Trees
A sparse Merkle tree represents a tree where most leaves are empty. Instead of storing all 2^256 possible leaves, we use these optimizations:
- Default hash values: Pre-compute the hash of an empty subtree at each level
- Lazy evaluation: Don’t store empty branches; reconstruct them as needed
- Compact proofs: Proofs can skip known-empty subtrees
Standard Merkle tree with 8 leaves (most empty):
R
/ \
A B
/ \ / \
C D E [empty subtree]
/ \
D1 D2
Sparse representation:
- Store only non-empty leaves: D1 at index 0, D2 at index 1
- Pre-computed empty subtrees: H_empty[0] = H(""), H_empty[1] = H(H_empty[0] || H_empty[0]), ...
This is critical for Ethereum’s state trie, which conceptually has 2^256 possible account addresses but only stores ~100 million actual accounts.
Merkle Trees in Bitcoin
Bitcoin uses Merkle trees for transaction ordering in blocks:
Block Header (80 bytes):
┌──────────────────────────┐
│ Version (4 bytes) │
│ Previous Block Hash (32) │
│ Merkle Root (32) │ ← This is our Merkle root!
│ Timestamp (4) │
│ Difficulty Target (4) │
│ Nonce (4) │
└──────────────────────────┘
Block Body:
┌──────────────────────────┐
│ Transaction Count │
│ Transactions... │ ← All hashed into Merkle root
└──────────────────────────┘
The Merkle root in the header commits to all transactions. Light clients can:
- Download headers only (80 bytes each)
- Request a specific transaction + proof from full nodes
- Verify inclusion against the header’s Merkle root
Merkle Trees in Ethereum
Ethereum uses three types of Merkle trees (actually Merkle Patricia Tries):
- State Trie: Maps addresses to account states
- Storage Trie: Each account has its own storage trie
- Transactions Trie: Transactions in each block
- Receipts Trie: Transaction receipts for each block
Block headers contain roots of all these tries, enabling proofs about any state.
Merkle Trees in Certificate Transparency
Certificate Transparency (CT) logs use Merkle trees to create publicly auditable logs of SSL/TLS certificates. This prevents CAs from secretly issuing fraudulent certificates.
Every certificate is added to an append-only Merkle tree. Anyone can:
- Get a proof that a certificate exists in the log
- Verify the log hasn’t been tampered with by checking the root
The Avalanche Effect in Merkle Trees
Like in hash functions, changing any leaf changes everything above it:
Original: D0 D1 D2 D3
↓ ↓ ↓ ↓
Hashes: H0 H1 H2 H3
\ / \ /
H01 H23
\ /
ROOT_A
Modified D2: D0 D1 D2' D3
↓ ↓ ↓ ↓
Hashes: H0 H1 H2' H3 ← H2 changed
\ / \ /
H01 H23' ← H23 changed
\ /
ROOT_B ← Root changed completely!
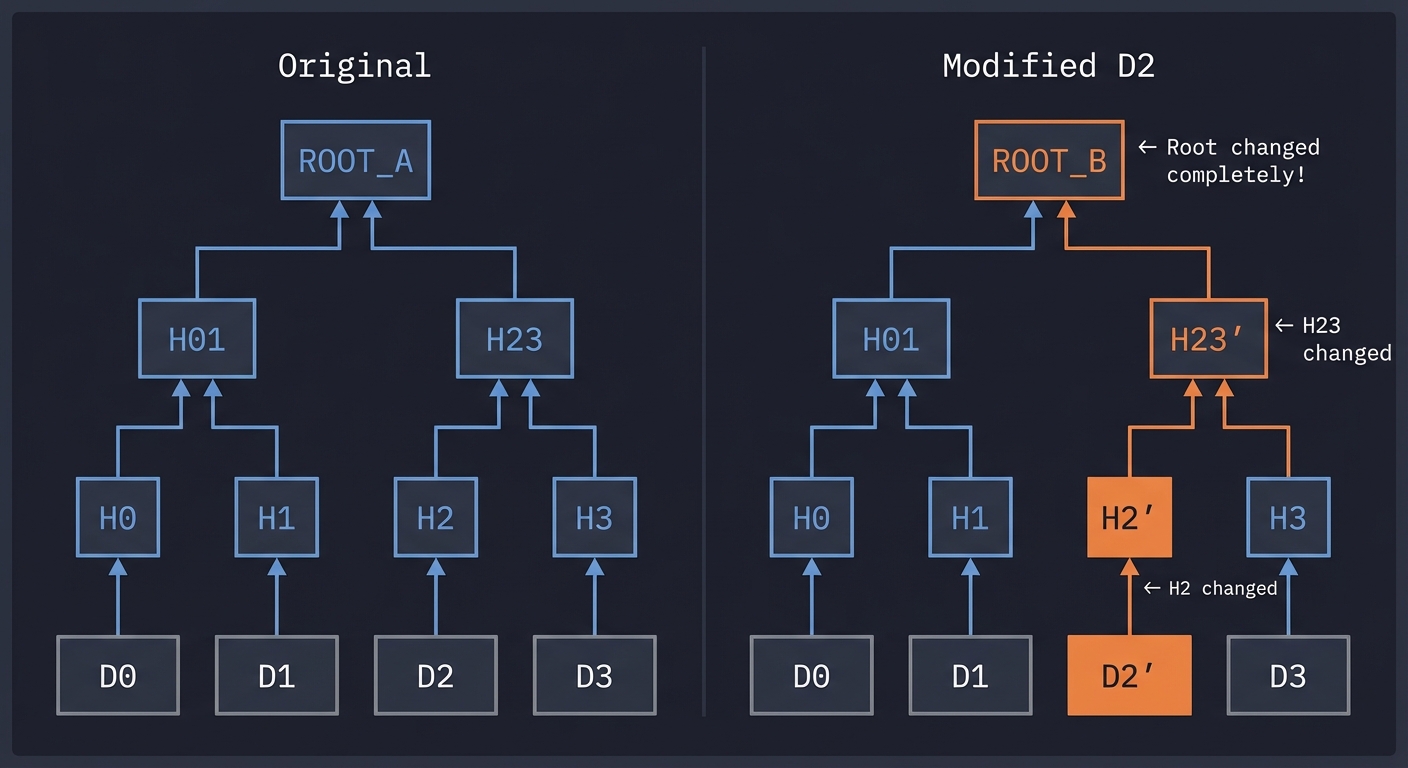
This is the foundation of tamper-evidence: any modification to any transaction changes the Merkle root in the block header, which invalidates the proof-of-work.
Complete Project Specification
Functional Requirements
- Tree Construction
- Build Merkle tree from arbitrary data items
- Handle any number of leaves (including odd counts)
- Support configurable hash function (SHA-256 default)
- Store tree structure for proof generation
- Proof Generation
- Generate inclusion proof for any leaf by index or content
- Return proof as list of sibling hashes with direction indicators
- Serialize proofs to portable format (JSON, binary)
- Proof Verification
- Verify proof against known root hash
- Return boolean result with detailed error information
- Support verification without access to full tree
- Visualization
- ASCII art display of tree structure
- Show how changing one leaf affects the root
- Highlight proof paths
- Sparse Merkle Trees (Extension)
- Efficient representation of mostly-empty trees
- Compact proofs for sparse data
- Support for non-membership proofs
Non-Functional Requirements
- Performance: Build tree of 1 million items in under 5 seconds
- Memory: Use O(n) memory for tree storage
- Correctness: Match Bitcoin/Ethereum test vectors
- Portability: Compile on Linux, macOS, Windows
Command-Line Interface
# Build tree from file (one item per line)
$ merkle build data.txt
Tree built with 1000 leaves
Root: a7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a
Height: 10 levels
# Build tree from inline data
$ merkle build --data "tx1" "tx2" "tx3" "tx4"
Root: 14ede5e8e97ad9372327728f5099b95604a39593cac3bd38a343ad76205213e7
# Generate proof for item at index
$ merkle proof --root a7ffc6f8... --index 42 --tree tree.json
Proof for index 42:
Sibling 0 (left): 3a7bd3e2360a3d...
Sibling 1 (right): 9f86d081884c...
...
Proof saved to proof.json
# Verify a proof
$ merkle verify --root a7ffc6f8... --data "tx42" --proof proof.json
✓ Proof VALID: "tx42" is in tree with root a7ffc6f8...
# Visualize tree structure
$ merkle visualize --tree tree.json
┌─────────────────────────────────┐
│ ROOT: 14ede5e8e97ad93... │
└─────────────────┬───────────────┘
│
┌───────────────────────┴────────────────────────┐
│ │
┌─────────┴─────────┐ ┌─────────┴─────────┐
│ c2355a6c7... │ │ c2355a6c7... │
└─────────┬─────────┘ └─────────┬─────────┘
│ │
┌─────────┴─────────┐ ┌─────────┴─────────┐
│ │ │ │ │ │
tx1 tx2 tx3 tx4
# Demonstrate avalanche effect
$ merkle avalanche --tree tree.json --modify 0 --new-data "tx1_modified"
Original root: 14ede5e8e97ad9372327728f5099b95604a39593cac3bd38a343ad76205213e7
Modified root: 8b5b3c7d9e2a1f4b5c6d7e8f9a0b1c2d3e4f5a6b7c8d9e0f1a2b3c4d5e6f7a8b
Changed nodes: 4/7 (57%)
Solution Architecture
Module Structure
merkle/
├── cmd/
│ └── merkle/
│ └── main.go # CLI entry point
├── pkg/
│ ├── tree/
│ │ ├── tree.go # Core MerkleTree type
│ │ ├── build.go # Tree construction
│ │ ├── proof.go # Proof generation
│ │ ├── verify.go # Proof verification
│ │ └── serialize.go # JSON/binary serialization
│ ├── sparse/
│ │ ├── sparse.go # Sparse Merkle tree
│ │ ├── defaults.go # Pre-computed empty hashes
│ │ └── compact.go # Compact proof format
│ ├── hash/
│ │ ├── hasher.go # Hash interface
│ │ └── sha256.go # SHA-256 implementation
│ └── visualize/
│ ├── ascii.go # ASCII tree rendering
│ └── diff.go # Change visualization
├── internal/
│ └── bits/
│ └── bits.go # Bit manipulation utilities
└── test/
├── vectors/
│ ├── bitcoin_test.go # Bitcoin test vectors
│ └── ethereum_test.go # Ethereum test vectors
└── tree_test.go # Unit tests
Core Data Structures
// Hash represents a 32-byte hash value
type Hash [32]byte
// Node represents a node in the Merkle tree
type Node struct {
Hash Hash
Left *Node
Right *Node
Parent *Node
Index int // Position at this level (0-indexed)
Level int // 0 = leaves, increases toward root
}
// MerkleTree represents a complete Merkle tree
type MerkleTree struct {
Root *Node
Leaves []*Node
Height int
LeafCount int
Hasher Hasher
}
// ProofStep represents one step in an inclusion proof
type ProofStep struct {
Hash Hash `json:"hash"`
IsLeft bool `json:"is_left"` // True if sibling is on the left
}
// Proof represents a complete Merkle inclusion proof
type Proof struct {
LeafHash Hash `json:"leaf_hash"`
LeafIndex int `json:"leaf_index"`
Steps []ProofStep `json:"steps"`
Root Hash `json:"root"`
}
// Hasher interface for pluggable hash functions
type Hasher interface {
Hash(data []byte) Hash
HashPair(left, right Hash) Hash
}
// SparseMerkleTree for efficient representation of mostly-empty trees
type SparseMerkleTree struct {
Root Hash
Depth int
Leaves map[uint64]Hash // Only non-empty leaves
DefaultHashes []Hash // Pre-computed empty subtree hashes
Hasher Hasher
}
Key Algorithms
Tree Construction
func BuildTree(data [][]byte, hasher Hasher) *MerkleTree {
if len(data) == 0 {
return &MerkleTree{Root: nil, Leaves: nil, Height: 0}
}
// Create leaf nodes
leaves := make([]*Node, len(data))
for i, item := range data {
leaves[i] = &Node{
Hash: hasher.Hash(item),
Index: i,
Level: 0,
}
}
// Handle odd number of leaves
if len(leaves) > 1 && len(leaves)%2 == 1 {
// Duplicate last leaf (Bitcoin style)
duplicate := &Node{
Hash: leaves[len(leaves)-1].Hash,
Index: len(leaves),
Level: 0,
}
leaves = append(leaves, duplicate)
}
// Build tree bottom-up
currentLevel := leaves
height := 0
for len(currentLevel) > 1 {
height++
nextLevel := make([]*Node, 0, len(currentLevel)/2)
for i := 0; i < len(currentLevel); i += 2 {
left := currentLevel[i]
right := currentLevel[i+1]
parent := &Node{
Hash: hasher.HashPair(left.Hash, right.Hash),
Left: left,
Right: right,
Index: i / 2,
Level: height,
}
left.Parent = parent
right.Parent = parent
nextLevel = append(nextLevel, parent)
}
// Handle odd number at this level
if len(nextLevel) > 1 && len(nextLevel)%2 == 1 {
last := nextLevel[len(nextLevel)-1]
duplicate := &Node{
Hash: last.Hash,
Index: len(nextLevel),
Level: height,
}
nextLevel = append(nextLevel, duplicate)
}
currentLevel = nextLevel
}
return &MerkleTree{
Root: currentLevel[0],
Leaves: leaves[:len(data)], // Original leaves only
Height: height,
LeafCount: len(data),
Hasher: hasher,
}
}
Proof Generation
func (t *MerkleTree) GenerateProof(leafIndex int) (*Proof, error) {
if leafIndex < 0 || leafIndex >= t.LeafCount {
return nil, fmt.Errorf("leaf index %d out of range [0, %d)", leafIndex, t.LeafCount)
}
leaf := t.Leaves[leafIndex]
proof := &Proof{
LeafHash: leaf.Hash,
LeafIndex: leafIndex,
Steps: make([]ProofStep, 0, t.Height),
Root: t.Root.Hash,
}
current := leaf
for current.Parent != nil {
parent := current.Parent
var sibling *Node
var isLeft bool
if parent.Left == current {
sibling = parent.Right
isLeft = false // Sibling is on the right
} else {
sibling = parent.Left
isLeft = true // Sibling is on the left
}
proof.Steps = append(proof.Steps, ProofStep{
Hash: sibling.Hash,
IsLeft: isLeft,
})
current = parent
}
return proof, nil
}
Proof Verification
func VerifyProof(proof *Proof, hasher Hasher) bool {
current := proof.LeafHash
for _, step := range proof.Steps {
if step.IsLeft {
current = hasher.HashPair(step.Hash, current)
} else {
current = hasher.HashPair(current, step.Hash)
}
}
return current == proof.Root
}
Phased Implementation Guide
Phase 1: Hash Interface and SHA-256
Goal: Set up the project and implement the hash function interface.
Tasks:
- Create Go module structure
- Define
Hashtype andHasherinterface - Implement SHA-256 hasher using crypto/sha256
- Implement
HashPairfor combining two hashes
Validation:
hasher := NewSHA256Hasher()
h := hasher.Hash([]byte("hello"))
// Should match: 2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824
Hints if stuck:
- Use
crypto/sha256package HashPairshould concatenate then hash:H(left || right)- Remember to handle byte order consistently
Phase 2: Basic Tree Construction
Goal: Build a Merkle tree from a list of data items.
Tasks:
- Implement
Nodestruct with hash storage - Create leaf nodes from data
- Build tree bottom-up, pairing nodes
- Handle power-of-2 leaf counts first
Validation:
data := [][]byte{[]byte("a"), []byte("b"), []byte("c"), []byte("d")}
tree := BuildTree(data, hasher)
// Manually compute expected root and verify
Hints if stuck:
- Start with exactly 4 leaves, then generalize
- Each level has half as many nodes as the previous
- Store parent pointers for later proof generation
Phase 3: Handling Odd Leaf Counts
Goal: Properly handle trees with non-power-of-2 leaf counts.
Tasks:
- Implement leaf duplication strategy
- Test with 3, 5, 7, etc. leaves
- Verify tree structure visually
Validation:
data := [][]byte{[]byte("a"), []byte("b"), []byte("c")}
tree := BuildTree(data, hasher)
// Tree should have 4 leaf nodes, with last duplicated
Hints if stuck:
- Duplicate at each level, not just at leaves
- Be careful with index tracking
- Write a function to print tree structure for debugging
Phase 4: Proof Generation
Goal: Generate inclusion proofs for any leaf.
Tasks:
- Navigate from leaf to root
- Collect sibling hashes at each level
- Record whether sibling is left or right
- Package as
Proofstruct
Validation:
proof, _ := tree.GenerateProof(2)
// Proof should have Height steps
// Each step should have valid sibling hash
Hints if stuck:
- Use parent pointers to traverse upward
- Sibling is
parent.Rightif current isparent.Left, vice versa - Include direction info for each step
Phase 5: Proof Verification
Goal: Verify a proof without access to the full tree.
Tasks:
- Start with leaf hash
- Apply each proof step, combining with sibling
- Compare final result with expected root
- Test with valid and invalid proofs
Validation:
valid := VerifyProof(proof, hasher)
assert(valid == true)
// Tamper with proof
proof.Steps[0].Hash[0] ^= 0xFF
valid = VerifyProof(proof, hasher)
assert(valid == false)
Hints if stuck:
- Direction matters!
H(left || right)is different fromH(right || left) - Use
IsLeftflag to determine concatenation order - Final hash must exactly equal root
Phase 6: Serialization and CLI
Goal: Save/load trees and proofs, create usable CLI.
Tasks:
- Implement JSON serialization for Proof
- Implement tree serialization (just leaves, rebuild on load)
- Create CLI commands: build, proof, verify
- Add file input support
Validation:
$ merkle build --data "a" "b" "c" "d" > tree.json
$ merkle proof --tree tree.json --index 2 > proof.json
$ merkle verify --proof proof.json --data "c"
✓ Valid
Hints if stuck:
- Use
encoding/jsonfor JSON - Serialize Hash as hex string
- Only need to store leaves to rebuild tree
Phase 7: Visualization and Demonstration
Goal: Visual output and avalanche demonstration.
Tasks:
- ASCII art tree rendering
- Highlight proof path
- Implement avalanche command
- Show changed vs unchanged nodes
Validation:
$ merkle visualize --tree tree.json
# Should show readable tree structure
$ merkle avalanche --tree tree.json --modify 0 --new "x"
# Should show percentage of changed nodes
Hints if stuck:
- Calculate column widths based on tree depth
- Use ANSI colors for highlighting
- Track which nodes change when rebuilding modified tree
Testing Strategy
Unit Tests
func TestBuildTree_Empty(t *testing.T) {
tree := BuildTree(nil, NewSHA256Hasher())
assert.Nil(t, tree.Root)
}
func TestBuildTree_SingleLeaf(t *testing.T) {
data := [][]byte{[]byte("only")}
tree := BuildTree(data, NewSHA256Hasher())
assert.Equal(t, 1, tree.LeafCount)
assert.Equal(t, 0, tree.Height)
}
func TestBuildTree_PowerOfTwo(t *testing.T) {
data := [][]byte{[]byte("a"), []byte("b"), []byte("c"), []byte("d")}
tree := BuildTree(data, NewSHA256Hasher())
assert.Equal(t, 4, tree.LeafCount)
assert.Equal(t, 2, tree.Height)
}
func TestBuildTree_OddCount(t *testing.T) {
data := [][]byte{[]byte("a"), []byte("b"), []byte("c")}
tree := BuildTree(data, NewSHA256Hasher())
assert.Equal(t, 3, tree.LeafCount)
// Internally has 4 nodes at leaf level
}
Proof Round-Trip Tests
func TestProofRoundTrip(t *testing.T) {
data := make([][]byte, 1000)
for i := range data {
data[i] = []byte(fmt.Sprintf("item-%d", i))
}
tree := BuildTree(data, NewSHA256Hasher())
for i := 0; i < len(data); i++ {
proof, err := tree.GenerateProof(i)
assert.NoError(t, err)
assert.True(t, VerifyProof(proof, NewSHA256Hasher()))
}
}
func TestProofInvalidation(t *testing.T) {
data := [][]byte{[]byte("a"), []byte("b"), []byte("c"), []byte("d")}
tree := BuildTree(data, NewSHA256Hasher())
proof, _ := tree.GenerateProof(2)
// Valid proof
assert.True(t, VerifyProof(proof, NewSHA256Hasher()))
// Tamper with sibling hash
proof.Steps[0].Hash[0] ^= 0xFF
assert.False(t, VerifyProof(proof, NewSHA256Hasher()))
}
Bitcoin Test Vectors
func TestBitcoinBlock170(t *testing.T) {
// Block 170 has 2 transactions
// This was the first block with a non-coinbase transaction
tx1 := hexDecode("0169...") // Coinbase TX hash
tx2 := hexDecode("f4184...") // First real TX hash
tree := BuildTree([][]byte{tx1, tx2}, NewDoubleSHA256Hasher())
expectedRoot := hexDecode("7dac2c56...")
assert.Equal(t, expectedRoot, tree.Root.Hash[:])
}
Performance Tests
func BenchmarkBuildTree1M(b *testing.B) {
data := make([][]byte, 1_000_000)
for i := range data {
data[i] = []byte(fmt.Sprintf("tx-%d", i))
}
b.ResetTimer()
for i := 0; i < b.N; i++ {
BuildTree(data, NewSHA256Hasher())
}
}
func BenchmarkProofGeneration(b *testing.B) {
data := make([][]byte, 1_000_000)
for i := range data {
data[i] = []byte(fmt.Sprintf("tx-%d", i))
}
tree := BuildTree(data, NewSHA256Hasher())
b.ResetTimer()
for i := 0; i < b.N; i++ {
tree.GenerateProof(i % len(data))
}
}
Common Pitfalls & Debugging
Pitfall 1: Wrong Concatenation Order
Problem: When verifying proofs, the order of concatenation matters. H(A || B) is not equal to H(B || A).
Symptom: Proofs verify in your code but not in reference implementations, or vice versa.
Solution:
// WRONG: Always putting current on left
current = hasher.HashPair(current, sibling)
// CORRECT: Use the direction flag
if step.IsLeft {
current = hasher.HashPair(step.Hash, current) // Sibling on left
} else {
current = hasher.HashPair(current, step.Hash) // Sibling on right
}
Pitfall 2: Odd Leaf Handling Inconsistency
Problem: Different implementations handle odd leaf counts differently. Bitcoin duplicates the last leaf; some implementations promote it.
Symptom: Root hash doesn’t match reference implementations.
Solution:
// Bitcoin style: duplicate last leaf
if len(nodes)%2 == 1 {
nodes = append(nodes, nodes[len(nodes)-1]) // Copy the node
}
// NOT: promoting the orphan directly (different result)
Pitfall 3: Index Tracking Through Levels
Problem: Losing track of node indices when building or traversing the tree.
Symptom: Wrong sibling selected in proof, off-by-one errors.
Solution:
// Track index at each level
type Node struct {
Index int // Position within this level
Level int // Height from leaves (0 = leaf)
}
// Parent index = child index / 2
parentIndex := currentIndex / 2
// Sibling index: flip the last bit
siblingIndex := currentIndex ^ 1
Pitfall 4: Bitcoin’s Double SHA-256
Problem: Bitcoin uses SHA256(SHA256(data)) for all hashing, not single SHA-256.
Symptom: Root hash doesn’t match Bitcoin block’s merkle root.
Solution:
func (h *DoubleSHA256Hasher) Hash(data []byte) Hash {
first := sha256.Sum256(data)
return sha256.Sum256(first[:])
}
func (h *DoubleSHA256Hasher) HashPair(left, right Hash) Hash {
combined := append(left[:], right[:]...)
return h.Hash(combined)
}
Pitfall 5: Memory Inefficiency for Large Trees
Problem: Storing full tree structure uses O(2n) memory.
Symptom: Out of memory for very large trees.
Solution:
// Option 1: Store only leaves, rebuild on demand
type CompactTree struct {
Leaves []Hash
Root Hash
}
// Option 2: Store level by level, discard intermediate nodes
func (t *CompactTree) GenerateProof(index int) *Proof {
// Rebuild path on the fly
proof := &Proof{}
current := t.Leaves
for len(current) > 1 {
// Get sibling
siblingIdx := index ^ 1
if siblingIdx < len(current) {
proof.Steps = append(proof.Steps, ProofStep{
Hash: current[siblingIdx],
IsLeft: index%2 == 1,
})
}
// Build next level
next := make([]Hash, (len(current)+1)/2)
for i := 0; i < len(current); i += 2 {
if i+1 < len(current) {
next[i/2] = hashPair(current[i], current[i+1])
} else {
next[i/2] = hashPair(current[i], current[i])
}
}
current = next
index /= 2
}
proof.Root = current[0]
return proof
}
Extensions and Challenges
Challenge 1: Sparse Merkle Trees
Implement a sparse Merkle tree that efficiently represents mostly-empty trees:
- Pre-compute default hashes for empty subtrees at each level
- Store only non-empty leaves in a map
- Generate proofs including default hash branches
- Support non-membership proofs (prove a key is NOT in the tree)
Challenge 2: Append-Only Merkle Trees
Implement a Merkle tree that supports efficient appending:
- Add new leaves without rebuilding the entire tree
- Maintain running root hash
- This is how Certificate Transparency logs work
Challenge 3: Merkle Mountain Ranges
Implement Merkle Mountain Ranges (MMR), used in Grin and other cryptocurrencies:
- Variable-height structure for append-only logs
- Efficient appending and proof generation
- Multiple “peaks” that get merged
Challenge 4: Parallel Tree Construction
Optimize tree building for multi-core systems:
- Hash leaves in parallel
- Build subtrees concurrently
- Merge at the end
- Target: build 1M leaves in under 1 second
Challenge 5: Merkle Patricia Trie
Implement a Merkle Patricia Trie as used in Ethereum:
- Combine Merkle tree with Patricia trie
- Support key-value storage with proofs
- Handle extension and branch nodes
Real-World Connections
Bitcoin Light Clients (SPV)
Your mobile Bitcoin wallet uses Merkle proofs to verify transactions without downloading the entire blockchain. When you receive Bitcoin:
- Your wallet downloads block headers (~50MB for all history)
- It requests the transaction + Merkle proof from a full node
- It verifies the proof against the header’s merkle root
- If valid, the transaction is confirmed
This is exactly what your library implements!
Ethereum State Proofs
Ethereum’s state trie (a modified Merkle Patricia Trie) enables:
- Proving an account’s balance without trusting the node
- Verifying smart contract storage
- Light client protocols like Helios
Certificate Transparency
Major browsers require certificates to be logged in CT logs, which are Merkle trees. Your library could:
- Verify a certificate is in a CT log
- Audit log consistency over time
- Detect if a log has been tampered with
Git Merkle DAG
Git uses a similar structure (Merkle DAG, not strictly a tree):
- Each commit hashes its tree and parent commits
- Any modification changes all downstream hashes
- This ensures repository integrity
IPFS Content Addressing
IPFS uses Merkle DAGs for content-addressed storage:
- Files are split into chunks, each with a hash
- Chunks are organized in a Merkle structure
- The root hash is the “CID” (Content Identifier)
Resources
Primary References
- “Mastering Bitcoin” Chapter 9 - Merkle Trees by Andreas Antonopoulos
- Original Merkle Patent (1979): US Patent 4309569
- Bitcoin Developer Reference: Merkle Trees
Code References
- Bitcoin Core Merkle Tree: GitHub
- go-merkletree: GitHub - Simple Go implementation
- Ethereum Patricia Trie: GitHub
Supplementary Reading
- Certificate Transparency: RFC 6962
- Sparse Merkle Trees: Efficient Sparse Merkle Trees
- Merkle Mountain Ranges: Grin Documentation
Interactive Learning
- Visualize Merkle Trees: blockchain-demo
- Build Your Own Blockchain: Learn Blockchains by Building One
Self-Assessment Checklist
Before moving to the next project, verify:
- I can explain why Merkle trees enable logarithmic proofs (O(log n) instead of O(n))
- I understand how to handle odd numbers of leaves and why different approaches exist
- I can generate a Merkle proof by hand for a small tree
- I can verify a Merkle proof given only the leaf, proof, and root (no full tree)
- I understand why changing one leaf changes the entire path to the root
- My implementation matches Bitcoin test vectors (double SHA-256)
- I can explain how light clients use Merkle proofs for SPV verification
- I understand the concept of sparse Merkle trees and when they’re useful
What’s Next?
With Merkle trees mastered, you understand one of the key data structures enabling trustless verification. In Project 4: Build a Blockchain from Scratch, you’ll combine hash functions, digital signatures, and Merkle trees to create a complete blockchain with blocks, transactions, and peer-to-peer networking. You’ll see how all these cryptographic primitives work together to create a decentralized, tamper-evident ledger.