Project 11: BrainInABox - Your Own Deep Learning Library
The Core Question: “How do frameworks like PyTorch and Keras work internally?”
Metadata
| Property | Value |
|---|---|
| Difficulty | Level 5: Master |
| Time Estimate | 4 Weeks (80-120 hours) |
| Main Language | Python |
| Knowledge Area | API Design / Software Architecture / Deep Learning Frameworks |
| Main Books | “Deep Learning” by Goodfellow et al., “Fluent Python” by Luciano Ramalho |
| Prerequisites | Projects 5 (Autograd), 6 (MLP), 8 (MNIST), 9 (CNN) |
| Fun Factor | Maximum - you become a framework author |
Learning Objectives
By the end of this project, you will be able to:
- Design a clean, composable API for building neural networks
- Implement the Module abstraction pattern used by PyTorch
- Create a parameter tracking system that automatically collects trainable weights
- Build a Sequential container that chains layers together
- Develop an optimizer abstraction supporting SGD, Adam, and custom optimizers
- Construct a DataLoader with batching, shuffling, and iteration
- Implement model serialization (save/load) for persistence
- Write comprehensive tests that validate your library works end-to-end
- Explain the design decisions behind major ML frameworks
- Contribute to open-source ML projects with newfound understanding
The Core Question You’re Answering
“How do frameworks like PyTorch and Keras work internally?”
When you type model = nn.Sequential(nn.Linear(784, 128), nn.ReLU(), nn.Linear(128, 10)) in PyTorch, dozens of things happen automatically:
- Each layer’s weights are initialized
- Parameters are registered and tracked
- Forward propagation chains through layers
- Gradients flow backward automatically
- Optimizers know exactly which tensors to update
This isn’t magic. It’s careful software architecture combined with deep learning fundamentals. By building your own framework, you’ll understand:
- Why PyTorch’s
nn.Modulehas methods likeparameters()andmodules() - How Keras knows to call each layer’s
__call__method in sequence - What happens inside
model.compile()andmodel.fit() - Why saving a model requires both architecture and weights
This capstone project proves you didn’t just copy code from earlier projects - you understand the abstraction. You can compose the pieces into a general-purpose learning machine.
Concepts You Must Understand First
1. API Design Principles
A good API is:
- Intuitive: Users guess correctly what functions do
- Consistent: Similar operations have similar interfaces
- Minimal: Expose only what’s necessary
- Composable: Small pieces combine into larger structures
Bad API: Good API:
layer.set_inputs(x) y = layer(x)
layer.compute()
y = layer.get_outputs()
Why? Good API is one line, intuitive, follows function-call pattern.
2. Module Abstraction (Layers as Objects)
In deep learning frameworks, everything is a “module”:
- A single layer is a module
- A network of layers is also a module
- Modules can contain other modules (composition)
Module Pattern:
class Module:
def __init__(self):
self._parameters = {}
self._modules = {}
def forward(self, x):
raise NotImplementedError
def __call__(self, x):
return self.forward(x)
def parameters(self):
# Return all trainable parameters
pass
3. The Training Loop Abstraction
Every training loop follows the same pattern:
for epoch in epochs:
for batch in data_loader:
# 1. Forward pass
predictions = model(batch.inputs)
# 2. Compute loss
loss = loss_fn(predictions, batch.targets)
# 3. Backward pass
loss.backward()
# 4. Update weights
optimizer.step()
# 5. Zero gradients
optimizer.zero_grad()
The fit() method encapsulates this loop, abstracting away the boilerplate.
4. Optimizer Design Patterns
Optimizers follow the Strategy Pattern:
- All optimizers have
step()andzero_grad() - Different optimizers (SGD, Adam) implement different update rules
- The training loop doesn’t care which optimizer is used
Optimizer Hierarchy:
Optimizer (base)
/ | \
SGD Adam RMSprop
All have: step(), zero_grad()
Each implements different weight update formula.
5. DataLoader and Batching
Training on one sample at a time is noisy. Training on all samples is slow. Batching is the sweet spot:
DataLoader Responsibilities:
1. Split data into batches of size N
2. Shuffle data each epoch (optional)
3. Provide iterator interface (for batch in loader)
4. Handle end-of-data (incomplete last batch)
6. Callbacks and Hooks
Callbacks allow injecting custom behavior into training:
class EarlyStopping:
def on_epoch_end(self, epoch, logs):
if logs['val_loss'] < self.best:
self.best = logs['val_loss']
self.wait = 0
else:
self.wait += 1
if self.wait >= self.patience:
model.stop_training = True
Deep Theoretical Foundation
PyTorch’s nn.Module Design
PyTorch’s nn.Module is a masterpiece of API design. Here’s how it works:
class Module:
def __init__(self):
# These store child modules and parameters
self._modules = OrderedDict()
self._parameters = OrderedDict()
def __setattr__(self, name, value):
# MAGIC: When you do self.layer = Linear(...)
# PyTorch intercepts and registers it!
if isinstance(value, Parameter):
self._parameters[name] = value
elif isinstance(value, Module):
self._modules[name] = value
else:
object.__setattr__(self, name, value)
def parameters(self):
# Recursively yield all parameters
for param in self._parameters.values():
yield param
for module in self._modules.values():
for param in module.parameters():
yield param
Key insight: The __setattr__ hook automatically tracks layers and parameters. When you write self.fc1 = Linear(10, 5), PyTorch registers both the module and its weights.
Keras’s Sequential vs Functional API
Sequential API (what we’ll build):
model = Sequential([
Linear(784, 128),
ReLU(),
Linear(128, 10)
])
Pros: Simple, clean for linear stacks Cons: Can’t handle multi-input or skip connections
Functional API:
inputs = Input(shape=(784,))
x = Linear(128)(inputs)
x = ReLU()(x)
outputs = Linear(10)(x)
model = Model(inputs, outputs)
Pros: Handles any graph structure Cons: More complex implementation
State Management: Parameters vs Buffers
Not all tensors in a model should be trained:
Parameters (trainable):
- Weight matrices
- Bias vectors
- Embedding tables
Buffers (not trainable, but saved):
- BatchNorm running mean/variance
- Fixed positional encodings
Neither (ephemeral):
- Intermediate activations
- Cached computations
PyTorch uses register_parameter() vs register_buffer() to distinguish these.
The Optimizer Abstraction
All optimizers share this interface:
class Optimizer:
def __init__(self, parameters, lr):
self.parameters = list(parameters)
self.lr = lr
def zero_grad(self):
for p in self.parameters:
p.grad = 0
def step(self):
raise NotImplementedError
SGD:
for p in parameters:
p.data -= lr * p.grad
Adam:
for p in parameters:
m = beta1 * m + (1 - beta1) * p.grad
v = beta2 * v + (1 - beta2) * p.grad^2
m_hat = m / (1 - beta1^t)
v_hat = v / (1 - beta2^t)
p.data -= lr * m_hat / (sqrt(v_hat) + epsilon)
DataLoader: Shuffling, Batching, Workers
DataLoader Pipeline:
Raw Data [X, Y]
│
▼
Shuffling (randomize order each epoch)
│
▼
Batching (group into chunks of batch_size)
│
▼
Iterator (yield one batch at a time)
│
▼
[Optional: Multiple workers for parallel loading]
Why shuffle? Without shuffling, the model might learn spurious order patterns. Shuffling ensures each epoch sees data in a different order.
Callbacks: EarlyStopping, ModelCheckpoint
Callbacks hook into the training loop at specific points:
Training Loop with Callbacks:
on_train_begin()
for epoch in epochs:
on_epoch_begin(epoch)
for batch in loader:
on_batch_begin(batch)
# ... training step ...
on_batch_end(batch, logs)
on_epoch_end(epoch, logs)
on_train_end()
Common callbacks:
- EarlyStopping: Stop if validation loss doesn’t improve
- ModelCheckpoint: Save model when validation loss improves
- LearningRateScheduler: Decay learning rate over time
- TensorBoard: Log metrics for visualization
Device Abstraction (CPU/GPU)
Frameworks abstract hardware:
# User doesn't write CUDA code directly
model = model.to('cuda') # Move to GPU
x = x.to('cuda') # Move data to GPU
y = model(x) # Computation happens on GPU
For this project: We’ll use NumPy (CPU only). GPU support via CuPy is an extension.
Serialization (Save/Load)
Saving a model requires two things:
- Architecture: The structure of layers and their configurations
- Weights: The learned parameter values
# Save
{
'architecture': model.get_config(), # How to rebuild
'weights': model.state_dict() # The learned values
}
# Load
model = Model.from_config(saved['architecture'])
model.load_state_dict(saved['weights'])
Real World Outcome
When you complete this project, you will have a working deep learning library. Here’s what using it looks like:
# This code should WORK with YOUR library:
import braininabox as bb
from braininabox.data import DataLoader
# Load MNIST data (you'll need to handle this externally)
X_train, y_train = load_mnist_train() # Shape: (60000, 784), (60000,)
X_test, y_test = load_mnist_test()
# Define model
model = bb.Sequential([
bb.layers.Linear(784, 128),
bb.layers.ReLU(),
bb.layers.Linear(128, 64),
bb.layers.ReLU(),
bb.layers.Linear(64, 10)
])
# Show model summary
print(model)
# Output:
# Sequential(
# (0): Linear(in_features=784, out_features=128)
# (1): ReLU()
# (2): Linear(in_features=128, out_features=64)
# (3): ReLU()
# (4): Linear(in_features=64, out_features=10)
# )
# Total parameters: 109,386
# Compile
model.compile(
optimizer=bb.optimizers.Adam(lr=0.001),
loss=bb.loss.CrossEntropy()
)
# Create data loader
train_loader = DataLoader(X_train, y_train, batch_size=32, shuffle=True)
# Train
history = model.fit(train_loader, epochs=10, verbose=True)
# Output:
# Epoch 1/10: loss=2.3012, accuracy=0.1234 [=====> ]
# Epoch 2/10: loss=0.8234, accuracy=0.7456 [=====> ]
# ...
# Epoch 10/10: loss=0.1234, accuracy=0.9678 [==============>]
# Evaluate
test_loader = DataLoader(X_test, y_test, batch_size=32)
test_loss, test_acc = model.evaluate(test_loader)
print(f"Test accuracy: {test_acc:.4f}")
# Predict
predictions = model.predict(X_test[:5])
print(f"Predictions: {predictions.argmax(axis=1)}")
# Save model
model.save('mnist_model.bb')
# Later: Load and use
loaded_model = bb.load('mnist_model.bb')
new_predictions = loaded_model.predict(X_test[:5])
Solution Architecture
Package Structure
braininabox/
├── __init__.py # Package exports (bb.Sequential, bb.layers, etc.)
├── tensor.py # Value class with autograd (from Project 5)
├── parameter.py # Parameter wrapper for trainable tensors
├── module.py # Base Module class
├── layers/
│ ├── __init__.py # Export all layers
│ ├── base.py # Layer base class
│ ├── linear.py # Fully connected layer
│ ├── conv.py # Conv2D layer
│ ├── pooling.py # MaxPool layer
│ ├── activation.py # ReLU, Sigmoid, Softmax
│ └── container.py # Sequential container
├── loss/
│ ├── __init__.py
│ ├── mse.py # Mean Squared Error
│ └── cross_entropy.py # Cross-Entropy Loss
├── optimizers/
│ ├── __init__.py
│ ├── base.py # Optimizer base class
│ ├── sgd.py # Stochastic Gradient Descent
│ └── adam.py # Adam optimizer
├── data/
│ ├── __init__.py
│ └── dataloader.py # DataLoader class
├── callbacks/
│ ├── __init__.py
│ ├── base.py # Callback base class
│ └── builtin.py # EarlyStopping, ModelCheckpoint
└── utils/
├── __init__.py
├── serialization.py # Save/load functionality
└── initializers.py # Weight initialization
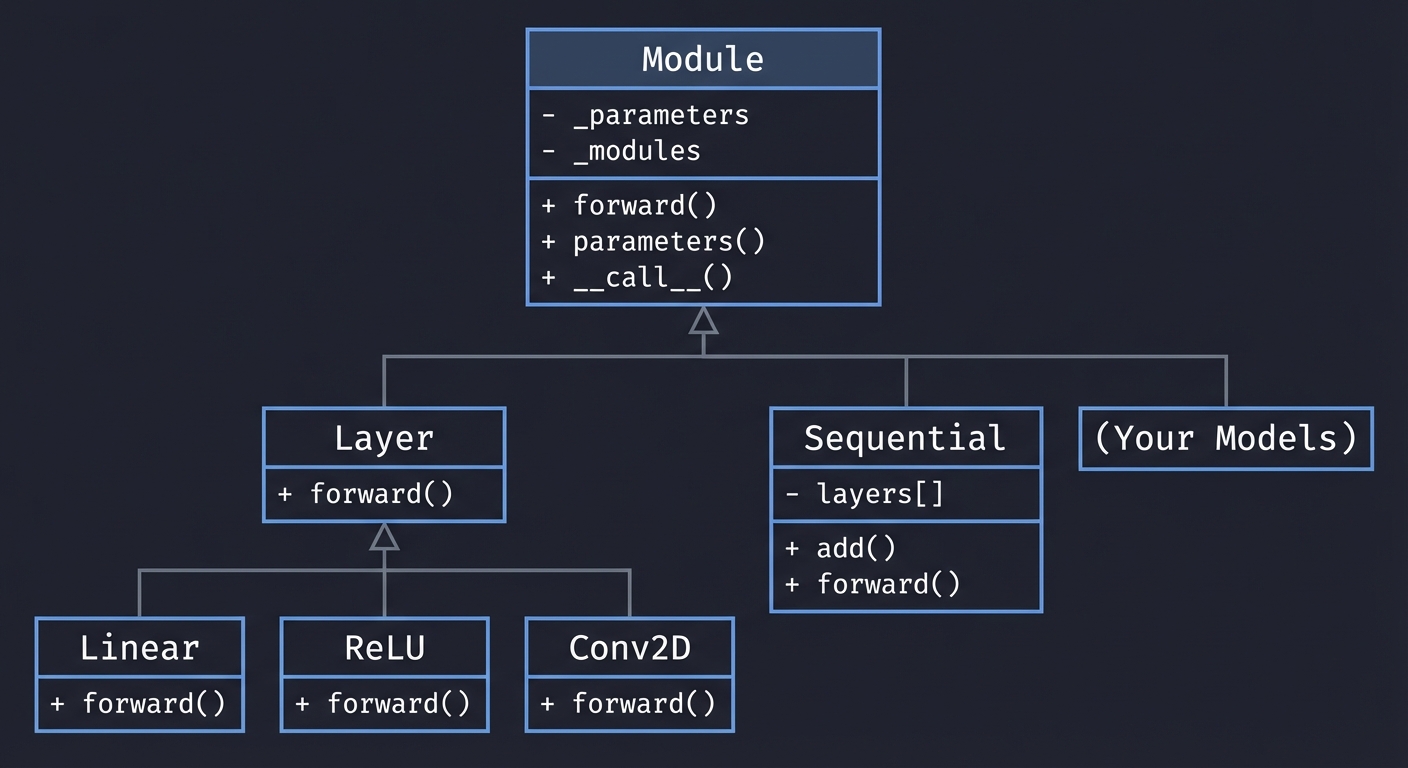
Class Hierarchy Diagram
+------------------+
| Module |
|------------------|
| - _parameters |
| - _modules |
| + forward() |
| + parameters() |
| + __call__() |
+--------+---------+
|
+----------------------+----------------------+
| | |
+-------v--------+ +--------v--------+ +--------v--------+
| Layer | | Sequential | | (Your Models) |
|----------------| |-----------------| |-----------------|
| + forward() | | - layers[] | | Inherits Module |
+-------+--------+ | + add() | +-----------------+
| | + forward() |
+-------+-------+ +-----------------+
| | |
+---v--+ +--v---+ +-v------+
|Linear| | ReLU | | Conv2D |
+------+ +------+ +--------+
+------------------+
| Optimizer |
|------------------|
| - parameters |
| - lr |
| + step() |
| + zero_grad() |
+--------+---------+
|
+----------------+----------------+
| |
+-------v--------+ +--------v--------+
| SGD | | Adam |
|----------------| |-----------------|
| + step() | | - m, v (moments)|
+----------------+ | + step() |
+-----------------+
+------------------+
| LossFunction |
|------------------|
| + forward() |
| + __call__() |
+--------+---------+
|
+----------------+----------------+
| |
+-------v--------+ +--------v--------+
| MSE | | CrossEntropy |
+----------------+ +-----------------+
Phased Implementation Guide
Phase 1: Package Structure Setup
Goal: Create the directory structure and init.py files.
mkdir -p braininabox/{layers,loss,optimizers,data,callbacks,utils}
touch braininabox/__init__.py
touch braininabox/{layers,loss,optimizers,data,callbacks,utils}/__init__.py
braininabox/__init__.py:
from .module import Module
from .layers.container import Sequential
from . import layers
from . import loss
from . import optimizers
from . import data
from .utils.serialization import load
__version__ = '0.1.0'
Deliverable: Running import braininabox as bb works without errors.
Phase 2: Base Tensor/Value Class (Autograd)
Goal: Port your autograd engine from Project 5.
Your Value class (or Tensor class) should support:
- Basic operations: +, -, *, /, **
- Broadcasting for scalar operations
- Gradient tracking
backward()method
# braininabox/tensor.py
class Value:
def __init__(self, data, _children=(), _op=''):
self.data = data
self.grad = 0.0
self._backward = lambda: None
self._prev = set(_children)
self._op = _op
def __add__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data + other.data, (self, other), '+')
def _backward():
self.grad += out.grad
other.grad += out.grad
out._backward = _backward
return out
def __mul__(self, other):
other = other if isinstance(other, Value) else Value(other)
out = Value(self.data * other.data, (self, other), '*')
def _backward():
self.grad += other.data * out.grad
other.grad += self.data * out.grad
out._backward = _backward
return out
# ... more operations ...
def backward(self):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
self.grad = 1.0
for node in reversed(topo):
node._backward()
Alternative: Use NumPy arrays as data and implement gradient tracking at the array level. This is more efficient for batch operations.
Deliverable: The following works:
x = Value(2.0)
y = Value(3.0)
z = x * y + x
z.backward()
assert x.grad == 4.0 # dz/dx = y + 1 = 3 + 1
assert y.grad == 2.0 # dz/dy = x = 2
Phase 3: Parameter and Module Base Class
Goal: Create the foundation for all layers and models.
Parameter: A wrapper that marks a tensor as trainable.
# braininabox/parameter.py
class Parameter:
"""A tensor that should be trained."""
def __init__(self, data):
self.data = data # NumPy array
self.grad = None
def zero_grad(self):
self.grad = None
Module: The base class for all neural network components.
# braininabox/module.py
class Module:
"""Base class for all neural network modules."""
def __init__(self):
self._parameters = {}
self._modules = {}
self.training = True
def __setattr__(self, name, value):
if isinstance(value, Parameter):
self.__dict__.setdefault('_parameters', {})[name] = value
elif isinstance(value, Module):
self.__dict__.setdefault('_modules', {})[name] = value
object.__setattr__(self, name, value)
def forward(self, *args, **kwargs):
raise NotImplementedError
def __call__(self, *args, **kwargs):
return self.forward(*args, **kwargs)
def parameters(self):
"""Yield all parameters (including from child modules)."""
for param in self._parameters.values():
yield param
for module in self._modules.values():
for param in module.parameters():
yield param
def modules(self):
"""Yield all child modules."""
yield self
for module in self._modules.values():
for m in module.modules():
yield m
def train(self):
"""Set to training mode."""
self.training = True
for module in self._modules.values():
module.train()
def eval(self):
"""Set to evaluation mode."""
self.training = False
for module in self._modules.values():
module.eval()
def __repr__(self):
return f"{self.__class__.__name__}()"
Deliverable: This works:
class DummyModule(Module):
def __init__(self):
super().__init__()
self.weight = Parameter(np.random.randn(10, 5))
def forward(self, x):
return x @ self.weight.data
m = DummyModule()
params = list(m.parameters())
assert len(params) == 1
assert params[0].data.shape == (10, 5)
Phase 4: Layer Implementations
Goal: Build the common layers.
Linear Layer:
# braininabox/layers/linear.py
import numpy as np
from ..module import Module
from ..parameter import Parameter
class Linear(Module):
"""Fully connected layer: y = xW + b"""
def __init__(self, in_features, out_features, bias=True):
super().__init__()
self.in_features = in_features
self.out_features = out_features
# Xavier initialization
bound = np.sqrt(6.0 / (in_features + out_features))
self.weight = Parameter(
np.random.uniform(-bound, bound, (in_features, out_features))
)
if bias:
self.bias = Parameter(np.zeros(out_features))
else:
self.bias = None
# Cache for backward pass
self._input = None
def forward(self, x):
self._input = x
out = x @ self.weight.data
if self.bias is not None:
out = out + self.bias.data
return out
def backward(self, grad_output):
"""Compute gradients and return gradient w.r.t. input."""
# Gradient w.r.t. weights: x^T @ grad_output
self.weight.grad = self._input.T @ grad_output
# Gradient w.r.t. bias: sum over batch
if self.bias is not None:
self.bias.grad = grad_output.sum(axis=0)
# Gradient w.r.t. input: grad_output @ W^T
return grad_output @ self.weight.data.T
def __repr__(self):
return f"Linear(in_features={self.in_features}, out_features={self.out_features})"
ReLU Activation:
# braininabox/layers/activation.py
import numpy as np
from ..module import Module
class ReLU(Module):
"""ReLU activation: max(0, x)"""
def __init__(self):
super().__init__()
self._mask = None
def forward(self, x):
self._mask = (x > 0)
return x * self._mask
def backward(self, grad_output):
return grad_output * self._mask
def __repr__(self):
return "ReLU()"
class Sigmoid(Module):
"""Sigmoid activation: 1 / (1 + exp(-x))"""
def __init__(self):
super().__init__()
self._output = None
def forward(self, x):
self._output = 1 / (1 + np.exp(-np.clip(x, -500, 500)))
return self._output
def backward(self, grad_output):
return grad_output * self._output * (1 - self._output)
class Softmax(Module):
"""Softmax activation: exp(x) / sum(exp(x))"""
def __init__(self, axis=-1):
super().__init__()
self.axis = axis
self._output = None
def forward(self, x):
# Numerical stability: subtract max
exp_x = np.exp(x - np.max(x, axis=self.axis, keepdims=True))
self._output = exp_x / np.sum(exp_x, axis=self.axis, keepdims=True)
return self._output
def backward(self, grad_output):
# Jacobian of softmax is complex; often combined with cross-entropy
# For standalone, this is an approximation
s = self._output
return grad_output * s * (1 - s)
Flatten Layer:
class Flatten(Module):
"""Flatten all dimensions except batch."""
def __init__(self):
super().__init__()
self._input_shape = None
def forward(self, x):
self._input_shape = x.shape
return x.reshape(x.shape[0], -1)
def backward(self, grad_output):
return grad_output.reshape(self._input_shape)
Conv2D (simplified):
# braininabox/layers/conv.py
import numpy as np
from ..module import Module
from ..parameter import Parameter
class Conv2D(Module):
"""2D Convolution layer."""
def __init__(self, out_channels, kernel_size, stride=1, padding=0):
super().__init__()
self.out_channels = out_channels
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
self.in_channels = None # Set on first forward
# Weights initialized lazily
self.weight = None
self.bias = Parameter(np.zeros(out_channels))
self._input = None
def _init_weights(self, in_channels):
self.in_channels = in_channels
k = self.kernel_size
bound = np.sqrt(6.0 / (in_channels * k * k + self.out_channels))
self.weight = Parameter(
np.random.uniform(-bound, bound, (self.out_channels, in_channels, k, k))
)
def forward(self, x):
# x shape: (batch, channels, height, width)
if self.weight is None:
self._init_weights(x.shape[1])
self._input = x
# ... convolution implementation ...
# (Use im2col for efficiency)
return self._convolve(x)
def _convolve(self, x):
# Implement convolution using im2col or loops
pass
def backward(self, grad_output):
# Compute weight and input gradients
pass
Deliverable: Each layer can do forward and backward passes:
layer = Linear(10, 5)
x = np.random.randn(3, 10) # batch of 3
y = layer(x)
assert y.shape == (3, 5)
grad = np.ones((3, 5))
dx = layer.backward(grad)
assert dx.shape == (3, 10)
assert layer.weight.grad.shape == (10, 5)
Phase 5: Loss Functions
Goal: Implement MSE and CrossEntropy with backward passes.
# braininabox/loss/mse.py
import numpy as np
class MSELoss:
"""Mean Squared Error Loss."""
def __init__(self):
self._diff = None
def __call__(self, predictions, targets):
return self.forward(predictions, targets)
def forward(self, predictions, targets):
self._diff = predictions - targets
return np.mean(self._diff ** 2)
def backward(self):
"""Returns gradient w.r.t. predictions."""
n = self._diff.size
return 2 * self._diff / n
# braininabox/loss/cross_entropy.py
import numpy as np
class CrossEntropyLoss:
"""Cross-Entropy Loss with built-in softmax."""
def __init__(self):
self._probs = None
self._targets = None
def __call__(self, logits, targets):
return self.forward(logits, targets)
def forward(self, logits, targets):
# Softmax
exp_logits = np.exp(logits - np.max(logits, axis=-1, keepdims=True))
self._probs = exp_logits / np.sum(exp_logits, axis=-1, keepdims=True)
# Store targets (one-hot or indices)
self._targets = targets
# Cross-entropy
batch_size = logits.shape[0]
if targets.ndim == 1:
# Targets are class indices
log_probs = -np.log(self._probs[np.arange(batch_size), targets] + 1e-8)
else:
# Targets are one-hot
log_probs = -np.sum(targets * np.log(self._probs + 1e-8), axis=-1)
return np.mean(log_probs)
def backward(self):
"""Returns gradient w.r.t. logits."""
batch_size = self._probs.shape[0]
grad = self._probs.copy()
if self._targets.ndim == 1:
grad[np.arange(batch_size), self._targets] -= 1
else:
grad = grad - self._targets
return grad / batch_size
Deliverable: Loss functions compute correct gradients.
Phase 6: Optimizer Base and SGD
Goal: Create the optimizer abstraction and SGD implementation.
# braininabox/optimizers/base.py
class Optimizer:
"""Base class for all optimizers."""
def __init__(self, parameters, lr=0.01):
self.parameters = list(parameters)
self.lr = lr
def zero_grad(self):
"""Reset all gradients to zero."""
for param in self.parameters:
param.grad = None
def step(self):
"""Update parameters. Override in subclasses."""
raise NotImplementedError
# braininabox/optimizers/sgd.py
from .base import Optimizer
class SGD(Optimizer):
"""Stochastic Gradient Descent with optional momentum."""
def __init__(self, parameters, lr=0.01, momentum=0.0):
super().__init__(parameters, lr)
self.momentum = momentum
self.velocities = [None] * len(self.parameters)
def step(self):
for i, param in enumerate(self.parameters):
if param.grad is None:
continue
if self.momentum > 0:
if self.velocities[i] is None:
self.velocities[i] = param.grad.copy()
else:
self.velocities[i] = (
self.momentum * self.velocities[i] + param.grad
)
param.data -= self.lr * self.velocities[i]
else:
param.data -= self.lr * param.grad
Deliverable: Optimizer updates parameters correctly.
Phase 7: Adam Optimizer
Goal: Implement the Adam optimizer.
# braininabox/optimizers/adam.py
import numpy as np
from .base import Optimizer
class Adam(Optimizer):
"""Adam optimizer with adaptive learning rates."""
def __init__(self, parameters, lr=0.001, beta1=0.9, beta2=0.999, eps=1e-8):
super().__init__(parameters, lr)
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.t = 0
self.m = [np.zeros_like(p.data) for p in self.parameters] # First moment
self.v = [np.zeros_like(p.data) for p in self.parameters] # Second moment
def step(self):
self.t += 1
for i, param in enumerate(self.parameters):
if param.grad is None:
continue
g = param.grad
# Update biased first moment estimate
self.m[i] = self.beta1 * self.m[i] + (1 - self.beta1) * g
# Update biased second raw moment estimate
self.v[i] = self.beta2 * self.v[i] + (1 - self.beta2) * (g ** 2)
# Compute bias-corrected first moment estimate
m_hat = self.m[i] / (1 - self.beta1 ** self.t)
# Compute bias-corrected second raw moment estimate
v_hat = self.v[i] / (1 - self.beta2 ** self.t)
# Update parameters
param.data -= self.lr * m_hat / (np.sqrt(v_hat) + self.eps)
Deliverable: Adam converges faster than vanilla SGD on test problems.
Phase 8: DataLoader
Goal: Build a DataLoader for batching and shuffling.
# braininabox/data/dataloader.py
import numpy as np
class DataLoader:
"""Iterates over data in batches."""
def __init__(self, X, y, batch_size=32, shuffle=True):
self.X = np.array(X)
self.y = np.array(y)
self.batch_size = batch_size
self.shuffle = shuffle
self.n_samples = len(X)
def __len__(self):
"""Number of batches per epoch."""
return (self.n_samples + self.batch_size - 1) // self.batch_size
def __iter__(self):
indices = np.arange(self.n_samples)
if self.shuffle:
np.random.shuffle(indices)
for start in range(0, self.n_samples, self.batch_size):
end = min(start + self.batch_size, self.n_samples)
batch_indices = indices[start:end]
yield self.X[batch_indices], self.y[batch_indices]
Deliverable: DataLoader iterates correctly:
X = np.random.randn(100, 10)
y = np.random.randint(0, 5, 100)
loader = DataLoader(X, y, batch_size=32, shuffle=True)
for batch_x, batch_y in loader:
assert batch_x.shape[0] <= 32
assert batch_x.shape[1] == 10
Phase 9: Sequential Container
Goal: Build the Sequential model that chains layers.
# braininabox/layers/container.py
import numpy as np
from ..module import Module
class Sequential(Module):
"""A sequential container of layers."""
def __init__(self, layers=None):
super().__init__()
self.layers = []
self._compiled = False
self.optimizer = None
self.loss_fn = None
if layers:
for layer in layers:
self.add(layer)
def add(self, layer):
"""Add a layer to the sequence."""
idx = len(self.layers)
self.layers.append(layer)
# Register as child module
setattr(self, f'layer_{idx}', layer)
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x
def backward(self, grad):
"""Backpropagate through all layers in reverse order."""
for layer in reversed(self.layers):
grad = layer.backward(grad)
return grad
def compile(self, optimizer, loss):
"""Configure the model for training."""
self.optimizer = optimizer
self.loss_fn = loss
# Attach parameters to optimizer
self.optimizer.parameters = list(self.parameters())
# Re-initialize optimizer state for Adam
if hasattr(self.optimizer, 'm'):
self.optimizer.m = [np.zeros_like(p.data) for p in self.optimizer.parameters]
self.optimizer.v = [np.zeros_like(p.data) for p in self.optimizer.parameters]
self.optimizer.t = 0
self._compiled = True
def fit(self, data_loader, epochs=1, verbose=True, callbacks=None):
"""Train the model."""
if not self._compiled:
raise RuntimeError("Model must be compiled before training. Call model.compile()")
history = {'loss': [], 'accuracy': []}
callbacks = callbacks or []
for callback in callbacks:
callback.on_train_begin(self)
for epoch in range(epochs):
epoch_loss = 0
epoch_correct = 0
epoch_total = 0
for callback in callbacks:
callback.on_epoch_begin(epoch)
for batch_x, batch_y in data_loader:
# Forward pass
predictions = self.forward(batch_x)
# Compute loss
loss = self.loss_fn(predictions, batch_y)
epoch_loss += loss * len(batch_x)
# Compute accuracy (for classification)
if predictions.ndim > 1 and predictions.shape[1] > 1:
pred_classes = predictions.argmax(axis=1)
if batch_y.ndim == 1:
epoch_correct += (pred_classes == batch_y).sum()
else:
epoch_correct += (pred_classes == batch_y.argmax(axis=1)).sum()
epoch_total += len(batch_x)
# Backward pass
grad = self.loss_fn.backward()
self.backward(grad)
# Update weights
self.optimizer.step()
self.optimizer.zero_grad()
avg_loss = epoch_loss / epoch_total
accuracy = epoch_correct / epoch_total
history['loss'].append(avg_loss)
history['accuracy'].append(accuracy)
if verbose:
print(f"Epoch {epoch+1}/{epochs}: loss={avg_loss:.4f}, accuracy={accuracy:.4f}")
for callback in callbacks:
callback.on_epoch_end(epoch, {'loss': avg_loss, 'accuracy': accuracy})
for callback in callbacks:
callback.on_train_end()
return history
def evaluate(self, data_loader):
"""Evaluate the model on a dataset."""
self.eval()
total_loss = 0
correct = 0
total = 0
for batch_x, batch_y in data_loader:
predictions = self.forward(batch_x)
loss = self.loss_fn(predictions, batch_y)
total_loss += loss * len(batch_x)
if predictions.ndim > 1 and predictions.shape[1] > 1:
pred_classes = predictions.argmax(axis=1)
if batch_y.ndim == 1:
correct += (pred_classes == batch_y).sum()
else:
correct += (pred_classes == batch_y.argmax(axis=1)).sum()
total += len(batch_x)
self.train()
return total_loss / total, correct / total
def predict(self, x):
"""Generate predictions."""
self.eval()
result = self.forward(x)
self.train()
return result
def __repr__(self):
lines = ['Sequential(']
for i, layer in enumerate(self.layers):
lines.append(f' ({i}): {layer}')
lines.append(')')
total_params = sum(p.data.size for p in self.parameters())
lines.append(f'Total parameters: {total_params:,}')
return '\n'.join(lines)
Deliverable: Full training loop works:
model = Sequential([
Linear(10, 5),
ReLU(),
Linear(5, 2)
])
model.compile(optimizer=SGD(model.parameters(), lr=0.01), loss=CrossEntropyLoss())
history = model.fit(train_loader, epochs=5)
Phase 10: Compile and Fit API
This is already integrated into Sequential in Phase 9. Additional enhancements:
Progress Bar (optional):
def _progress_bar(current, total, width=40):
percent = current / total
filled = int(width * percent)
bar = '=' * filled + '>' + ' ' * (width - filled - 1)
return f'[{bar}] {current}/{total}'
Validation Split:
def fit(self, data_loader, epochs=1, validation_data=None, verbose=True):
# ... training code ...
if validation_data:
val_loss, val_acc = self.evaluate(validation_data)
if verbose:
print(f" val_loss={val_loss:.4f}, val_accuracy={val_acc:.4f}")
Phase 11: Save/Load Functionality
Goal: Persist and restore models.
# braininabox/utils/serialization.py
import pickle
import numpy as np
def save(model, path):
"""Save model architecture and weights."""
state = {
'class': model.__class__.__name__,
'layers': [],
'weights': {}
}
for i, layer in enumerate(model.layers):
layer_info = {
'class': layer.__class__.__name__,
'config': _get_layer_config(layer)
}
state['layers'].append(layer_info)
for name, param in model._parameters.items():
state['weights'][name] = param.data.copy()
for i, layer in enumerate(model.layers):
prefix = f'layer_{i}.'
for name, param in layer._parameters.items():
state['weights'][prefix + name] = param.data.copy()
with open(path, 'wb') as f:
pickle.dump(state, f)
def load(path):
"""Load a saved model."""
with open(path, 'rb') as f:
state = pickle.load(f)
# Reconstruct model
from ..layers import Linear, ReLU, Sigmoid, Softmax, Flatten
from ..layers.container import Sequential
layer_classes = {
'Linear': Linear,
'ReLU': ReLU,
'Sigmoid': Sigmoid,
'Softmax': Softmax,
'Flatten': Flatten,
}
layers = []
for layer_info in state['layers']:
cls = layer_classes[layer_info['class']]
config = layer_info['config']
if config:
layers.append(cls(**config))
else:
layers.append(cls())
model = Sequential(layers)
# Load weights
for name, data in state['weights'].items():
if name.startswith('layer_'):
parts = name.split('.')
layer_idx = int(parts[0].replace('layer_', ''))
param_name = parts[1]
getattr(model.layers[layer_idx], param_name).data = data
return model
def _get_layer_config(layer):
"""Extract configuration from a layer."""
if isinstance(layer, Linear):
return {
'in_features': layer.in_features,
'out_features': layer.out_features
}
return {}
Deliverable: Round-trip save/load works:
model.save('test.bb')
loaded = bb.load('test.bb')
assert np.allclose(model.predict(X), loaded.predict(X))
Phase 12: Testing Suite
Goal: Comprehensive tests for each component.
# tests/test_layers.py
import numpy as np
import unittest
from braininabox.layers import Linear, ReLU
from braininabox.parameter import Parameter
class TestLinear(unittest.TestCase):
def test_forward_shape(self):
layer = Linear(10, 5)
x = np.random.randn(3, 10)
y = layer(x)
self.assertEqual(y.shape, (3, 5))
def test_backward_shape(self):
layer = Linear(10, 5)
x = np.random.randn(3, 10)
y = layer(x)
grad = np.ones((3, 5))
dx = layer.backward(grad)
self.assertEqual(dx.shape, (3, 10))
self.assertEqual(layer.weight.grad.shape, (10, 5))
def test_gradient_numerical(self):
"""Verify gradients match numerical approximation."""
layer = Linear(4, 2)
x = np.random.randn(2, 4)
# Forward and backward
y = layer(x)
loss = y.sum()
grad = np.ones_like(y)
layer.backward(grad)
# Numerical gradient
eps = 1e-5
numerical_grad = np.zeros_like(layer.weight.data)
for i in range(layer.weight.data.shape[0]):
for j in range(layer.weight.data.shape[1]):
layer.weight.data[i, j] += eps
y_plus = layer(x).sum()
layer.weight.data[i, j] -= 2 * eps
y_minus = layer(x).sum()
layer.weight.data[i, j] += eps
numerical_grad[i, j] = (y_plus - y_minus) / (2 * eps)
np.testing.assert_allclose(
layer.weight.grad, numerical_grad, rtol=1e-4, atol=1e-4
)
class TestReLU(unittest.TestCase):
def test_forward(self):
relu = ReLU()
x = np.array([[-1, 0, 1], [2, -2, 0.5]])
y = relu(x)
expected = np.array([[0, 0, 1], [2, 0, 0.5]])
np.testing.assert_array_equal(y, expected)
def test_backward(self):
relu = ReLU()
x = np.array([[-1, 0, 1], [2, -2, 0.5]])
y = relu(x)
grad = np.ones_like(x)
dx = relu.backward(grad)
expected = np.array([[0, 0, 1], [1, 0, 1]])
np.testing.assert_array_equal(dx, expected)
# tests/test_sequential.py
class TestSequential(unittest.TestCase):
def test_forward(self):
model = Sequential([
Linear(10, 5),
ReLU(),
Linear(5, 2)
])
x = np.random.randn(3, 10)
y = model(x)
self.assertEqual(y.shape, (3, 2))
def test_parameter_count(self):
model = Sequential([
Linear(10, 5), # 10*5 + 5 = 55
ReLU(), # 0
Linear(5, 2) # 5*2 + 2 = 12
])
total = sum(p.data.size for p in model.parameters())
self.assertEqual(total, 67)
# tests/test_optimizers.py
class TestSGD(unittest.TestCase):
def test_step(self):
param = Parameter(np.array([1.0, 2.0]))
param.grad = np.array([0.1, 0.2])
opt = SGD([param], lr=0.1)
opt.step()
expected = np.array([0.99, 1.98])
np.testing.assert_allclose(param.data, expected)
class TestAdam(unittest.TestCase):
def test_convergence(self):
"""Adam should converge on a simple quadratic."""
param = Parameter(np.array([5.0]))
opt = Adam([param], lr=0.1)
for _ in range(100):
param.grad = 2 * param.data # gradient of x^2
opt.step()
self.assertAlmostEqual(param.data[0], 0.0, places=2)
if __name__ == '__main__':
unittest.main()
Deliverable: All tests pass:
python -m pytest tests/ -v
Questions to Guide Your Design
Answer these before coding:
-
How does PyTorch’s
nn.Moduleautomatically find all parameters? Hint: Look at__setattr__and recursion through child modules. -
Why does the backward pass go through layers in REVERSE order? Hint: Chain rule - you need the gradient from the next layer to compute this layer’s gradient.
-
What’s the difference between
model.parameters()andmodel.state_dict()? Hint: One yields Parameter objects, the other yields their data as a dictionary. -
Why does Adam have
m_hat = m / (1 - beta1^t)correction? Hint: What happens tomin the first few steps when it’s initialized to zero? -
How would you add support for
model.to('cuda')using CuPy? Hint: What would need to change in Parameter and Layer classes? -
Why do we set
model.eval()before inference? Hint: Think about Dropout and BatchNorm layers. -
How would you implement a skip connection (like ResNet)? Hint: Sequential can’t do this - you need a different API.
Thinking Exercise: Design a Functional API
The Sequential API is limited. Design (on paper) a Functional API that could handle:
# Skip connection (ResNet style)
inputs = bb.Input(shape=(784,))
x = bb.layers.Linear(128)(inputs)
x = bb.layers.ReLU()(x)
skip = x # Save for later
x = bb.layers.Linear(128)(x)
x = bb.layers.ReLU()(x)
x = bb.layers.Add()([x, skip]) # Skip connection!
outputs = bb.layers.Linear(10)(x)
model = bb.Model(inputs, outputs)
Questions to answer:
- How do layers know their input shapes before seeing data?
- How do you track the computation graph?
- How does backward work with multiple paths?
Testing Strategy
Unit Tests for Each Component
| Component | Test Cases |
|---|---|
| Linear | Forward shape, backward shape, numerical gradient check |
| ReLU | Forward values, backward mask |
| CrossEntropy | Forward loss value, backward gradient |
| SGD | Single step update, momentum accumulation |
| Adam | Bias correction, convergence on quadratic |
| DataLoader | Batch sizes, shuffling randomness, last batch handling |
| Sequential | Forward propagation, parameter collection, save/load |
Integration Tests
def test_mnist_training():
"""Full end-to-end test on MNIST subset."""
# Load 1000 samples
X, y = load_mnist_subset(1000)
model = bb.Sequential([
bb.layers.Linear(784, 64),
bb.layers.ReLU(),
bb.layers.Linear(64, 10)
])
model.compile(
optimizer=bb.optimizers.Adam(lr=0.01),
loss=bb.loss.CrossEntropy()
)
loader = DataLoader(X, y, batch_size=32)
history = model.fit(loader, epochs=5, verbose=False)
# Should achieve > 80% accuracy
assert history['accuracy'][-1] > 0.8
Gradient Checking
For every layer, verify backward matches numerical gradient:
def gradient_check(layer, x, eps=1e-5):
y = layer(x)
grad = np.ones_like(y)
analytical = layer.backward(grad)
numerical = np.zeros_like(x)
for i in np.ndindex(x.shape):
x_plus = x.copy()
x_plus[i] += eps
x_minus = x.copy()
x_minus[i] -= eps
numerical[i] = (layer(x_plus).sum() - layer(x_minus).sum()) / (2 * eps)
return np.allclose(analytical, numerical, rtol=1e-4)
Common Pitfalls and Debugging Tips
Pitfall 1: Gradients Not Propagating
Symptom: Weights don’t change after training
Cause: Forgetting to call backward() on layers, or not connecting optimizer to parameters.
Debug:
for param in model.parameters():
print(f"Grad: {param.grad}") # Should not be None after backward
Pitfall 2: In-Place Modification During Backward
Symptom: Incorrect gradients, especially with shared weights
Cause: Modifying arrays in place instead of creating new ones
Fix:
# BAD
self.grad += incoming_grad
# GOOD
self.grad = (self.grad if self.grad is not None else 0) + incoming_grad
Pitfall 3: Forgetting to Zero Gradients
Symptom: Gradients accumulate across batches, training diverges
Cause: Not calling optimizer.zero_grad() each iteration
Fix: Always zero gradients at the start or end of each batch.
Pitfall 4: Shape Mismatches in Backward
Symptom: ValueError: operands could not be broadcast together
Cause: Not handling batch dimension correctly in gradients
Debug:
def backward(self, grad_output):
print(f"grad_output shape: {grad_output.shape}")
print(f"_input shape: {self._input.shape}")
# ...
Pitfall 5: Numerical Instability in Softmax/CrossEntropy
Symptom: NaN or Inf values during training
Cause: Exponentiating large numbers
Fix:
# BAD
exp_x = np.exp(x)
# GOOD (subtract max for stability)
exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))
Pitfall 6: Optimizer State Not Matching Parameters
Symptom: Adam doesn’t work after modifying model
Cause: Optimizer’s moment vectors have wrong shape
Fix: Re-initialize optimizer or use model.compile() which handles this.
Interview Questions
When you understand this project, you can answer:
Q1: “How does PyTorch track gradients?”
Answer: PyTorch uses a dynamic computation graph. Each tensor operation creates a node in the graph that remembers the operation and its inputs. When you call backward(), PyTorch traverses the graph in reverse order using topological sort, applying the chain rule to compute gradients for each node.
Q2: “Explain the difference between model.parameters() and model.state_dict()”
Answer:
parameters()yields Parameter objects that contain both data and gradient information. Used for optimizer construction.state_dict()returns a dictionary mapping parameter names to their data (NumPy/Tensor). Used for serialization. It also includes buffers (non-trainable state like BatchNorm running averages).
Q3: “Why do we need separate forward and backward passes?”
Answer: The forward pass computes the output and caches intermediate values needed for gradients. The backward pass uses these cached values along with the incoming gradient to compute gradients for parameters and inputs. They must be separate because (1) we often want inference without gradients, and (2) the backward pass needs the forward results.
Q4: “How would you implement weight sharing between two layers?”
Answer: Have both layers reference the same Parameter object. During backward, both layers will contribute to that parameter’s gradient. The optimizer will update it once, affecting both layers.
Q5: “Why does Adam often work better than SGD?”
Answer: Adam combines three improvements:
- Momentum: Accumulates gradient direction, powering through local noise
- Adaptive learning rates: Scales updates by inverse of gradient magnitude history
- Bias correction: Compensates for zero initialization of moment estimates
This helps with: sparse gradients, noisy data, saddle points, and ill-conditioned loss surfaces.
Q6: “What happens during model.compile() in Keras?”
Answer: It configures the model for training by:
- Associating an optimizer with the model’s parameters
- Setting the loss function
- Setting up metrics for tracking
- Potentially building the graph (in TensorFlow backend)
- Allocating memory for training state
Hints in Layers
If stuck, reveal these progressively:
Hint 1: Module Registration
The key to automatic parameter tracking is __setattr__:
def __setattr__(self, name, value):
if isinstance(value, Parameter):
self._parameters[name] = value
elif isinstance(value, Module):
self._modules[name] = value
object.__setattr__(self, name, value)
Make sure _parameters and _modules exist before this is called (initialize in __init__ before calling super().__init__()).
Hint 2: Sequential Forward/Backward
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x
def backward(self, grad):
for layer in reversed(self.layers):
grad = layer.backward(grad)
return grad
Hint 3: Linear Layer Backward
For y = xW + b:
dL/dW = x^T @ dL/dydL/db = sum(dL/dy, axis=0)dL/dx = dL/dy @ W^T
def backward(self, grad_output):
self.weight.grad = self._input.T @ grad_output
self.bias.grad = grad_output.sum(axis=0)
return grad_output @ self.weight.data.T
Hint 4: CrossEntropy Backward with Softmax
When softmax is built into cross-entropy, the gradient simplifies:
# For class indices (not one-hot)
grad = softmax_output.copy()
grad[np.arange(batch_size), targets] -= 1
grad /= batch_size
Hint 5: Adam Moment Initialization
def __init__(self, parameters, lr=0.001, beta1=0.9, beta2=0.999, eps=1e-8):
super().__init__(parameters, lr)
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.t = 0
self.m = [np.zeros_like(p.data) for p in self.parameters]
self.v = [np.zeros_like(p.data) for p in self.parameters]
Hint 6: Save/Load Architecture
Store layer class names and their constructor arguments:
{
'layers': [
{'class': 'Linear', 'config': {'in_features': 784, 'out_features': 128}},
{'class': 'ReLU', 'config': {}},
...
],
'weights': {
'layer_0.weight': np.array(...),
'layer_0.bias': np.array(...),
...
}
}
Extensions and Challenges
Extension 1: Add GPU Support (CuPy)
Replace NumPy with CuPy for GPU acceleration:
try:
import cupy as cp
HAS_GPU = True
except ImportError:
import numpy as cp
HAS_GPU = False
class Parameter:
def to(self, device):
if device == 'cuda' and HAS_GPU:
self.data = cp.asarray(self.data)
elif device == 'cpu':
self.data = cp.asnumpy(self.data) if HAS_GPU else self.data
Extension 2: Implement Callbacks
class Callback:
def on_train_begin(self, model): pass
def on_train_end(self): pass
def on_epoch_begin(self, epoch): pass
def on_epoch_end(self, epoch, logs): pass
def on_batch_begin(self, batch): pass
def on_batch_end(self, batch, logs): pass
class EarlyStopping(Callback):
def __init__(self, patience=5, monitor='val_loss'):
self.patience = patience
self.monitor = monitor
self.best = float('inf')
self.wait = 0
def on_epoch_end(self, epoch, logs):
current = logs.get(self.monitor, logs.get('loss'))
if current < self.best:
self.best = current
self.wait = 0
else:
self.wait += 1
if self.wait >= self.patience:
print(f"Early stopping at epoch {epoch}")
raise StopIteration
Extension 3: Add Regularization (L1, L2)
class Linear(Module):
def __init__(self, in_f, out_f, weight_decay=0.0):
# ...
self.weight_decay = weight_decay
def backward(self, grad_output):
# Normal gradient
self.weight.grad = self._input.T @ grad_output
# Add L2 regularization gradient
if self.weight_decay > 0:
self.weight.grad += self.weight_decay * self.weight.data
# ...
Extension 4: Build a Functional API
class Input:
def __init__(self, shape):
self.shape = shape
self.output_shape = shape
self._outputs = []
class FunctionalLayer:
def __call__(self, inputs):
# Track connections
self._inputs = inputs
inputs._outputs.append(self)
return self
class Model:
def __init__(self, inputs, outputs):
self.inputs = inputs
self.outputs = outputs
self._build_graph()
def _build_graph(self):
# Traverse from outputs to inputs, build layer order
pass
Extension 5: Implement Dropout
class Dropout(Module):
def __init__(self, p=0.5):
super().__init__()
self.p = p
self._mask = None
def forward(self, x):
if self.training:
self._mask = (np.random.rand(*x.shape) > self.p) / (1 - self.p)
return x * self._mask
return x
def backward(self, grad_output):
return grad_output * self._mask
Extension 6: Implement BatchNorm
class BatchNorm(Module):
def __init__(self, num_features, momentum=0.1, eps=1e-5):
super().__init__()
self.gamma = Parameter(np.ones(num_features))
self.beta = Parameter(np.zeros(num_features))
self.running_mean = np.zeros(num_features)
self.running_var = np.ones(num_features)
self.momentum = momentum
self.eps = eps
Real-World Connections
Contributing to Open Source ML
After building BrainInABox, you’re ready to:
- Read PyTorch source code: The patterns will be familiar
- Contribute bug fixes: You understand the module system
- Add new layers: You know the forward/backward contract
- Debug training issues: You know what happens inside
fit()
Framework Design Trade-offs
| Design Choice | PyTorch | TensorFlow/Keras | Your Library |
|---|---|---|---|
| Graph type | Dynamic | Static (TF1) / Dynamic (TF2) | Dynamic |
| Eager execution | Yes | Optional | Yes |
| Device management | Explicit .to() |
Automatic | Explicit |
| Distributed training | torch.distributed | tf.distribute | Not implemented |
Production Considerations
Your library is educational, not production-ready. Real frameworks have:
- JIT compilation: Fuse operations for speed
- Distributed training: Multi-GPU, multi-machine
- Quantization: Reduce model size
- ONNX export: Interoperability
- Mobile deployment: TensorFlow Lite, PyTorch Mobile
Books That Will Help
| Book | Relevance |
|---|---|
| “Deep Learning” by Goodfellow et al. | The mathematical foundation for every layer |
| “Fluent Python” by Luciano Ramalho | Python magic methods, descriptors, metaclasses |
| “Clean Code” by Robert Martin | API design principles |
| “Design Patterns” by Gang of Four | Strategy (Optimizer), Composite (Module), Iterator (DataLoader) |
| PyTorch Source Code | The reference implementation |
Online Resources:
- PyTorch internals blog posts
- Andrej Karpathy’s micrograd
- TinyGrad by George Hotz
- JAX documentation on autodiff
Self-Assessment Checklist
Before considering this project complete, verify:
Understanding
- I can explain how
nn.Module.__setattr__enables automatic parameter tracking - I can draw the class hierarchy for Module, Layer, Sequential
- I understand why backward passes through layers in reverse order
- I can explain Adam’s bias correction formula
- I know why we call
optimizer.zero_grad()each iteration
Implementation
- All layers pass numerical gradient checks
- Sequential forward/backward works correctly
- SGD and Adam optimizers update parameters
- DataLoader shuffles and batches correctly
- Save/load round-trip preserves predictions
- Model trains on MNIST and achieves >90% accuracy
API Quality
- The API feels intuitive and consistent
- Error messages are helpful
- Model summary (
print(model)) is informative - Code is well-documented
Extensions
- I implemented at least one extension (callbacks, GPU, regularization)
- I can explain how to add a new layer type
- I understand the limitations of Sequential vs Functional API
Interview Ready
- I can whiteboard the Module pattern
- I can explain the training loop abstraction
- I can discuss framework design trade-offs
- I can read and understand PyTorch source code
What’s Next?
After completing BrainInABox, you have truly mastered the fundamentals. You are now ready to:
- Contribute to PyTorch/TensorFlow: You understand the architecture
- Build custom layers: For research or production
- Optimize performance: Add JIT, GPU kernels, quantization
- Explore advanced topics: Transformers, diffusion models, reinforcement learning
You are no longer just a user of deep learning frameworks. You are someone who could build one from scratch. That’s the difference between an operator and an engineer.
“Any sufficiently advanced abstraction is indistinguishable from magic - until you build it yourself.”