Linear Algebra Learning Projects - Deep Dive Series
Master linear algebra by building systems where matrices, vectors, and transformations aren’t abstractions—they’re the actual machinery.
This directory contains comprehensive, expanded guides for each project in the Linear Algebra Learning Projects curriculum. Each guide provides everything you need to deeply understand both the theory and implementation.
Learning Philosophy
Linear algebra is the mathematics of transformations and spaces. It’s the language computers use to manipulate graphics, train AI, process signals, and simulate physics. These projects are designed so that you cannot complete them without internalizing the core concepts—the math IS the implementation.
The Progression
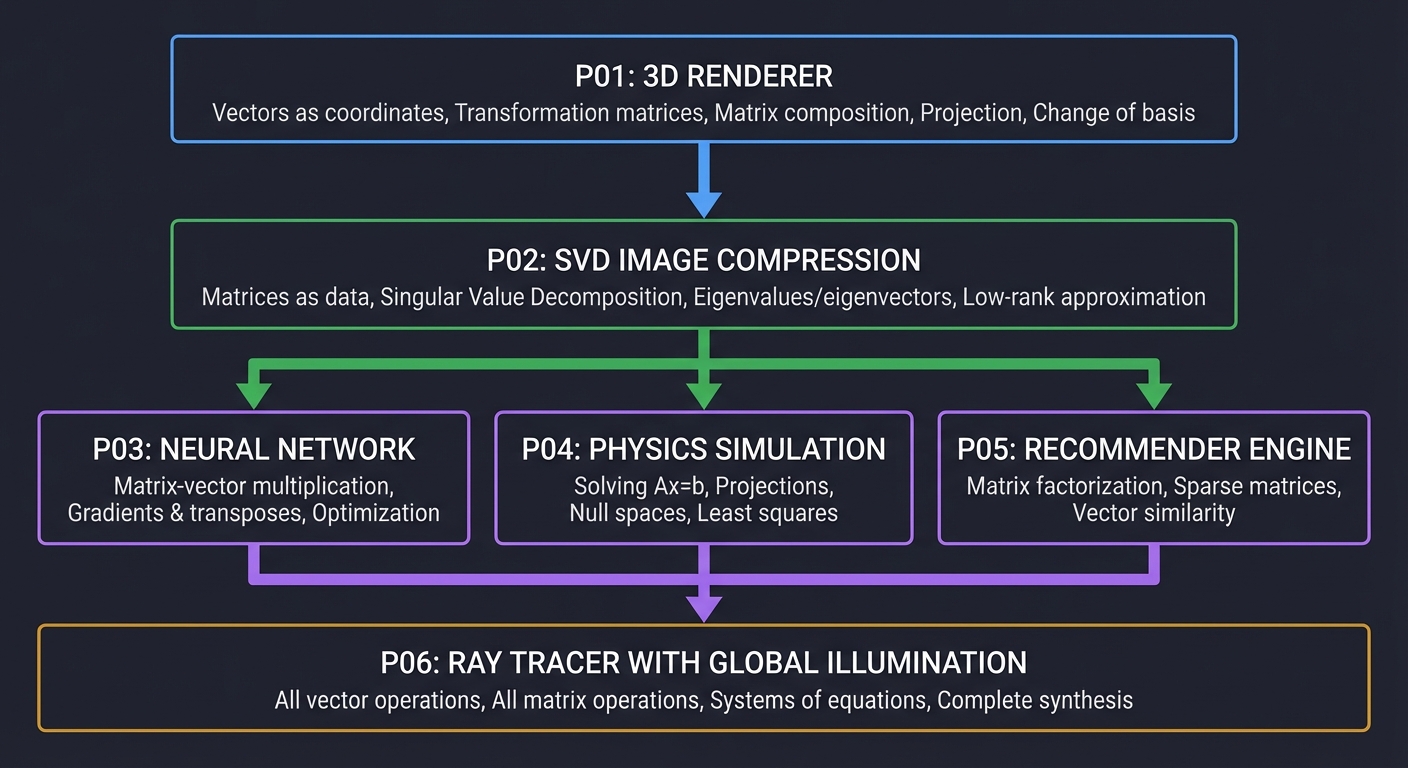
┌─────────────────────────────────────────────────────────────────────────────┐
│ LINEAR ALGEBRA MASTERY PATH │
├─────────────────────────────────────────────────────────────────────────────┤
│ │
│ FOUNDATION │
│ ───────── │
│ ┌─────────────────────────────────────────────────────────────────────┐ │
│ │ P01: 3D RENDERER │ │
│ │ • Vectors as coordinates │ │
│ │ • Transformation matrices (rotation, scale, translation) │ │
│ │ • Matrix composition │ │
│ │ • Projection and homogeneous coordinates │ │
│ │ • Change of basis (camera transforms) │ │
│ └─────────────────────────────────────────────────────────────────────┘ │
│ │ │
│ ▼ │
│ DECOMPOSITION & STRUCTURE │
│ ───────────────────────── │
│ ┌─────────────────────────────────────────────────────────────────────┐ │
│ │ P02: SVD IMAGE COMPRESSION │ │
│ │ • Matrices as data │ │
│ │ • Singular Value Decomposition │ │
│ │ • Eigenvalues/eigenvectors intuition │ │
│ │ • Low-rank approximation │ │
│ │ • Information content and rank │ │
│ └─────────────────────────────────────────────────────────────────────┘ │
│ │ │
│ ┌───────────────┼───────────────┐ │
│ ▼ ▼ ▼ │
│ APPLICATIONS (choose your path) │
│ ─────────────────────────────── │
│ ┌─────────────────┐ ┌─────────────────┐ ┌─────────────────┐ │
│ │ P03: NEURAL NET │ │ P04: PHYSICS │ │ P05: RECOMMENDER│ │
│ │ │ │ │ │ │ │
│ │ • Matrix-vector │ │ • Solving Ax=b │ │ • Matrix factor-│ │
│ │ multiplication│ │ • Projections │ │ ization │ │
│ │ • Gradients & │ │ • Null spaces │ │ • Sparse matrices│ │
│ │ transposes │ │ • Least squares │ │ • Vector similar-│ │
│ │ • Optimization │ │ • Conditioning │ │ ity │ │
│ └─────────────────┘ └─────────────────┘ └─────────────────┘ │
│ │ │ │ │
│ └───────────────┼───────────────┘ │
│ ▼ │
│ CAPSTONE │
│ ──────── │
│ ┌─────────────────────────────────────────────────────────────────────┐ │
│ │ P06: RAY TRACER WITH GLOBAL ILLUMINATION │ │
│ │ • All vector operations │ │
│ │ • All matrix operations │ │
│ │ • Solving systems of equations │ │
│ │ • Orthonormal basis construction │ │
│ │ • Everything synthesized into photorealistic rendering │ │
│ └─────────────────────────────────────────────────────────────────────┘ │
│ │
└─────────────────────────────────────────────────────────────────────────────┘
Project Index
| # | Project | Difficulty | Time | Core Concepts |
|---|---|---|---|---|
| P01 | Software 3D Renderer | Intermediate | 2-3 weeks | Transformations, matrices, projections |
| P02 | SVD Image Compression | Intermediate | 1-2 weeks | Decomposition, eigenvalues, rank |
| P03 | Neural Network from Scratch | Intermediate-Advanced | 2-3 weeks | Matrix multiplication, gradients |
| P04 | Physics Simulation | Advanced | 3-4 weeks | Systems of equations, projections |
| P05 | Recommendation Engine | Intermediate | 1-2 weeks | Factorization, similarity |
| P06 | Ray Tracer (Capstone) | Advanced | 1-2 months | Complete synthesis |
| P07 | Abstract Vector Space Axiom Testbench | Advanced | 1 week | Axioms, subspaces, basis/dimension |
| P08 | Proof-Driven FTLA Workbench | Advanced | 2 weeks | Rank-nullity, FTLA, proof contracts |
| P09 | Jordan/Rational Canonical Explorer | Advanced | 2-3 weeks | Canonical forms, similarity invariants |
| P10 | Invariant Subspace Spectral Lab | Advanced | 2-3 weeks | Spectral theorem, subspace stability |
| P11 | Inner Product/Bilinear Geometry Studio | Advanced | 2 weeks | Orthogonality, projections, metrics |
| P12 | Dual Space Functional Compiler | Advanced | 2 weeks | Dual maps, adjoints, covector transforms |
Core Concepts Map
Each project teaches specific linear algebra concepts. Here’s what you’ll master:
Vectors & Basic Operations
- What they are: Ordered lists of numbers representing points or directions in space
- Learned in: P01 (coordinates), P04 (physical state), P06 (rays)
- Key operations: Addition, scalar multiplication, dot product, cross product
Matrices & Transformations
- What they are: Transformation machines that map vectors to vectors
- Learned in: P01 (rotation/scale/projection), P03 (layer weights)
- Key operations: Matrix-vector multiplication, matrix-matrix multiplication
Matrix Decompositions
- What they are: Breaking matrices into simpler, meaningful pieces
- Learned in: P02 (SVD), P05 (factorization)
- Key types: LU, QR, SVD, Eigendecomposition
Systems of Linear Equations
- What they are: Finding vectors that satisfy multiple constraints
- Learned in: P04 (constraint solving), P06 (ray-object intersection)
- Key methods: Gaussian elimination, iterative solvers
Eigenvalues & Eigenvectors
- What they are: The “natural axes” of a transformation
- Learned in: P02 (singular values), P03 (weight initialization)
- Key insight: Directions that only scale under transformation
Abstract Vector Spaces & Proof Theory
- What they are: Coordinate-free structures and theorem-level reasoning
- Learned in: P07, P08
- Key insight: Algebraic contracts come before algorithms
Canonical Forms & Invariant Subspaces
- What they are: Similarity-class structure and decomposition guarantees
- Learned in: P09, P10
- Key insight: Operator identity survives basis changes
Bilinear Forms, Inner Products & Dual Spaces
- What they are: Metric-driven geometry and linear functionals
- Learned in: P11, P12
- Key insight: Vectors and covectors transform differently unless metric-identification is explicit
Recommended Learning Order
Path 1: Graphics Focus
P01 → P02 → P06
Best for: Game developers, graphics programmers, visualization enthusiasts
Path 2: Machine Learning Focus
P01 → P02 → P03 → P05
Best for: ML engineers, data scientists, AI researchers
Path 3: Simulation Focus
P01 → P04 → P06
Best for: Physics engine developers, scientific computing, robotics
Path 4: Complete Mastery
P01 → P02 → P03 → P04 → P05 → P06 → P07 → P08 → P09 → P10 → P11 → P12
Best for: Those who want comprehensive linear algebra mastery
Path 5: College-Theory Completion
P07 → P08 → P09 → P10 → P11 → P12
Best for: Learners who already know computational basics and want full abstract/theoretical depth
Essential Resources
Primary Learning Materials
- 3Blue1Brown: Essence of Linear Algebra (YouTube) - Geometric intuition
- “Computer Graphics from Scratch” by Gabriel Gambetta - Graphics applications
- “Math for Programmers” by Paul Orland - Programming-focused approach
Reference Materials
- “Linear Algebra Done Right” by Sheldon Axler - Rigorous theory
- “Numerical Recipes in C” by Press et al. - Numerical implementation
- “Physically Based Rendering” by Pharr & Humphreys - Advanced ray tracing
Tools
- Python + NumPy: Quick prototyping and verification
- C: Deep understanding through manual implementation
- GeoGebra: Visualizing transformations
- Desmos: Plotting and exploration
How to Use These Guides
Each expanded project guide contains:
- Learning Objectives - What you’ll understand after completion
- Theoretical Foundation - Deep enough to learn without other sources
- Project Specification - Exactly what you’re building
- Solution Architecture - Design guidance without spoiling implementation
- Phased Implementation - Step-by-step progression with checkpoints
- Testing Strategy - How to verify your implementation
- Common Pitfalls - Mistakes to avoid
- Extensions - Ways to deepen your learning
- Real-World Connections - Industry applications
- Self-Assessment - Verify your understanding
Getting Started
- Choose your path from the recommended orders above
- Start with P01 (required for all paths)
- Watch 3Blue1Brown Episode 1 before coding
- Read the theoretical foundation in your project guide
- Build incrementally - one concept at a time
- Verify understanding - can you explain each concept without notes?
Remember: The goal isn’t to finish projects quickly—it’s to reach the point where you see matrices as transformations, feel eigenvectors as natural axes, and think in terms of vector spaces.
Last updated: 2026