P06: Ray Tracer with Global Illumination (Capstone)
P06: Ray Tracer with Global Illumination (Capstone)
Build a ray tracer that renders photorealistic 3D scenes by simulating light bouncing through the environmentโsynthesizing all linear algebra concepts into one magnificent project.
Overview
| Attribute | Value |
|---|---|
| Difficulty | Advanced |
| Time Estimate | 1-2 months |
| Language | C (recommended) or C++/Rust |
| Prerequisites | Complete P01 (3D Renderer), recommended all previous projects |
| Primary Book | โComputer Graphics from Scratchโ + โPhysically Based Renderingโ |
Learning Objectives
This capstone project synthesizes EVERYTHING youโve learned:
- Vectors: Rays as origin + direction vectors
- Dot Products: Angle calculations for lighting
- Cross Products: Surface normal computation
- Matrices: Camera and object transformations
- Systems of Equations: Ray-object intersection
- Matrix Inverses: Transforming rays into object space
- Projections: Reflection and refraction vectors
- Orthonormal Bases: Sampling hemispheres for global illumination
Theoretical Foundation
Part 1: What is Ray Tracing?
The Core Idea
Instead of projecting 3D geometry to 2D (like P01), we trace rays FROM the camera INTO the scene:
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ RAY TRACING OVERVIEW โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโค
โ โ
โ Light Source โ
โ โ๏ธ โ
โ โฑโโฒ โ
โ โฑ โ โฒ โ
โ โฑ โ โฒ โ
โ โฑ โ โฒ โ
โ Object โ ๐กโโโโผโโโโถ (light bounces) โ
โ โฑโ โ โ
โ โฑ โฒ โ โ
โ โฑ โฒ โ โ
โ Camera โ ๐ทโโโโโโโ (ray from camera hits object) โ
โ ray intersection โ
โ โ
โ For each pixel: โ
โ 1. Cast ray from camera through pixel โ
โ 2. Find what it hits โ
โ 3. Calculate lighting at that point โ
โ 4. Set pixel color accordingly โ
โ โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
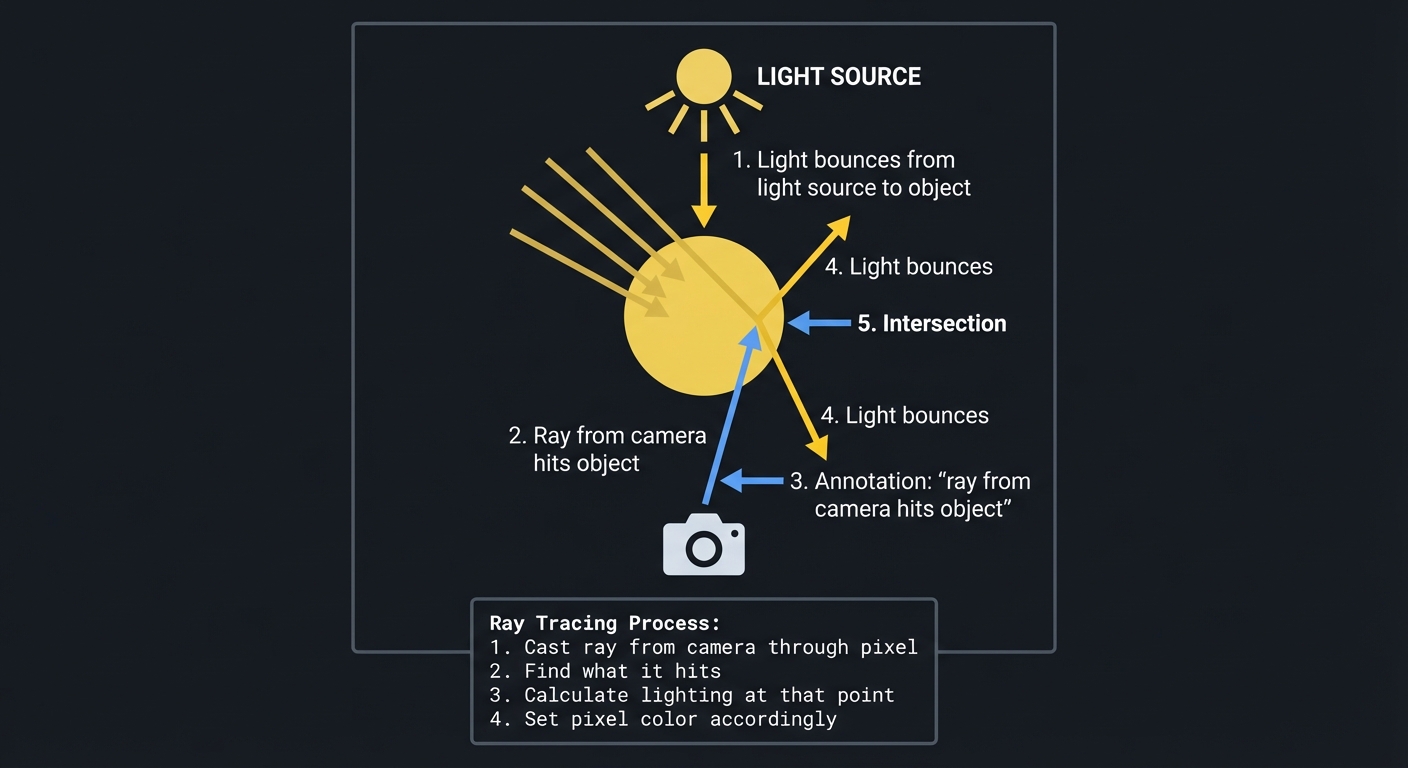
Why Ray Tracing?
- Physically accurate: Simulates how light actually works
- Handles reflections naturally: Just trace more rays
- Handles shadows naturally: Check if light reaches point
- Handles refraction naturally: Bend rays through glass
The Linear Algebra Connection
Every operation in ray tracing is linear algebra:
| Operation | Linear Algebra Concept |
|---|---|
| Ray definition | Vector (origin) + Vector (direction) |
| Ray-sphere intersection | Solving quadratic equation |
| Ray-plane intersection | Solving linear equation |
| Surface normal | Normalized vector perpendicular to surface |
| Lighting calculation | Dot product (cosine of angle) |
| Reflection | Vector projection and reflection formula |
| Refraction | Vector decomposition and Snellโs law |
| Camera positioning | Transformation matrices |
| Texture coordinates | Projection and interpolation |
Part 2: Rays and Intersections
Defining a Ray
A ray is a half-line: starting point + direction:
Ray: P(t) = O + t ร D, where t โฅ 0
O = origin point (camera or previous bounce point)
D = direction vector (should be normalized)
t = parameter (distance along ray)
P(t) = point on ray at distance t
For each pixel, we compute a primary ray:
For pixel (x, y) on screen:
direction = normalize(pixel_world_position - camera_position)
ray = Ray(camera_position, direction)
Ray-Sphere Intersection
A sphere: all points at distance r from center C:
Sphere: ||P - C||ยฒ = rยฒ
Substitute ray equation P = O + tD:
||O + tD - C||ยฒ = rยฒ
Let L = O - C (vector from sphere center to ray origin):
||L + tD||ยฒ = rยฒ
(L + tD) ยท (L + tD) = rยฒ
LยทL + 2t(LยทD) + tยฒ(DยทD) = rยฒ
Since D is normalized, DยทD = 1:
tยฒ + 2(LยทD)t + (LยทL - rยฒ) = 0
This is a quadratic: atยฒ + bt + c = 0
a = 1
b = 2(LยทD)
c = LยทL - rยฒ
discriminant = bยฒ - 4ac
If discriminant < 0: no intersection
If discriminant = 0: ray grazes sphere (one point)
If discriminant > 0: ray enters and exits (two points)
t = (-b ยฑ โdiscriminant) / 2a
Take the smallest positive t โ that's the closest intersection.
This is solving a quadratic equation derived from the sphere equation!
Ray-Plane Intersection
A plane: all points P where (P - Pโ) ยท N = 0
Plane: point Pโ on plane, normal N
Substitute ray: (O + tD - Pโ) ยท N = 0
(O - Pโ) ยท N + t(D ยท N) = 0
t = [(Pโ - O) ยท N] / [D ยท N]
If D ยท N = 0: ray parallel to plane (no intersection)
If D ยท N โ 0: solve for t
If t < 0: intersection is behind ray origin
This is solving a linear equation!
Ray-Triangle Intersection
Triangles are defined by three vertices A, B, C. Use barycentric coordinates:
Any point in triangle plane: P = A + u(B-A) + v(C-A)
= (1-u-v)A + uB + vC
Inside triangle when: u โฅ 0, v โฅ 0, u + v โค 1
Set P = O + tD and solve for t, u, v:
O + tD = A + u(B-A) + v(C-A)
This is a system of 3 linear equations in 3 unknowns!
Can solve with Cramer's rule or matrix inversion.
The Mรถller-Trumbore algorithm efficiently solves this using cross products.
Part 3: Surface Normals and Lighting
Computing Normals
The normal at an intersection tells us which way the surface faces:
Sphere: N = normalize(P - C) (points radially outward)
Plane: N is given (the plane normal)
Triangle: N = normalize((B-A) ร (C-A)) (cross product!)
Can also interpolate vertex normals for smooth shading
The Dot Product in Lighting
Lambertโs cosine law: brightness proportional to cos(ฮธ) where ฮธ is angle between light and normal:
Light
โ L
โฒ
ฮธ โฒ
โโโโโโโโโโโโโโโNโ (surface normal)
โ
surface
Intensity = max(0, N ยท L) ร light_color
If N ยท L > 0: surface faces light (illuminated)
If N ยท L = 0: light grazes surface (dark edge)
If N ยท L < 0: surface faces away (in shadow)
The dot product computes the cosine of the angle!
Phong Lighting Model
A simple but effective lighting model:
Color = Ambient + Diffuse + Specular
Ambient = ka ร ambient_color
(constant background illumination)
Diffuse = kd ร max(0, N ยท L) ร diffuse_color
(matte surface scattering)
Specular = ks ร max(0, R ยท V)^shininess ร specular_color
(shiny highlights)
Where:
- N = surface normal
- L = direction to light
- V = direction to viewer (camera)
- R = reflection of L about N
Computing the reflection vector R:
R = 2(N ยท L)N - L
This is the reflection formula from P01!
Part 4: Shadows
Shadow Rays
To check if a point is in shadow:
1. At intersection point P, cast a ray toward the light
2. If this ray hits another object before reaching the light โ shadow
3. If nothing blocks it โ illuminated
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ SHADOW COMPUTATION โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโค
โ โ
โ Light โ
โ โ๏ธ โ
โ โฑ โ
โ โฑ โ
โ โฑ โ
โ Blocker โณ โ shadow ray blocked! โ
โ ๐ค โฑ โ
โ โฑ โ
โ โฑ โ
โ โ P (intersection point) โ
โ โ
โ Point P is in shadow because an object blocks the light. โ
โ โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
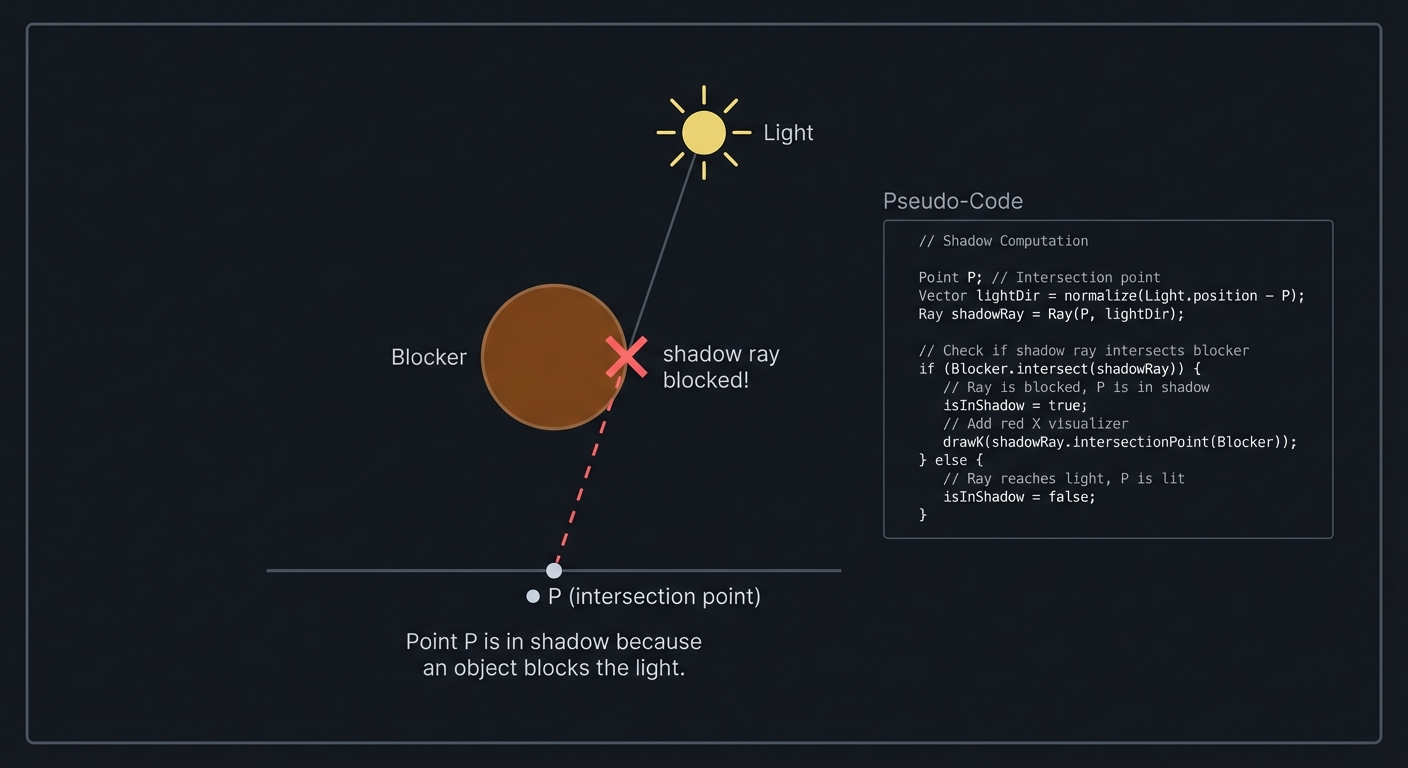
Shadow = testing for intersection, the same linear algebra!
Soft Shadows
For soft shadows, treat light as an area (not a point):
Sample multiple points on the light source
For each sample, cast a shadow ray
Average results โ partial shadow (penumbra)
Part 5: Reflection and Refraction
Perfect Reflection (Mirrors)
For reflective surfaces, trace a reflected ray:
Reflection direction: R = D - 2(D ยท N)N
Where D is incoming ray direction, N is surface normal.
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ REFLECTION โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโค
โ โ
โ Incoming ray D โ
โ โ โ
โ โฒ โ
โ ฮธ โฒ ฮธ โ
โ โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ surface โ
โ โฑโ โ
โ โฑ โN (normal) โ
โ โฑ โ โ
โ โ โ โ
โ Reflected ray R โ
โ โ
โ angle in = angle out (measured from normal) โ
โ R = D - 2(DยทN)N โ
โ โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
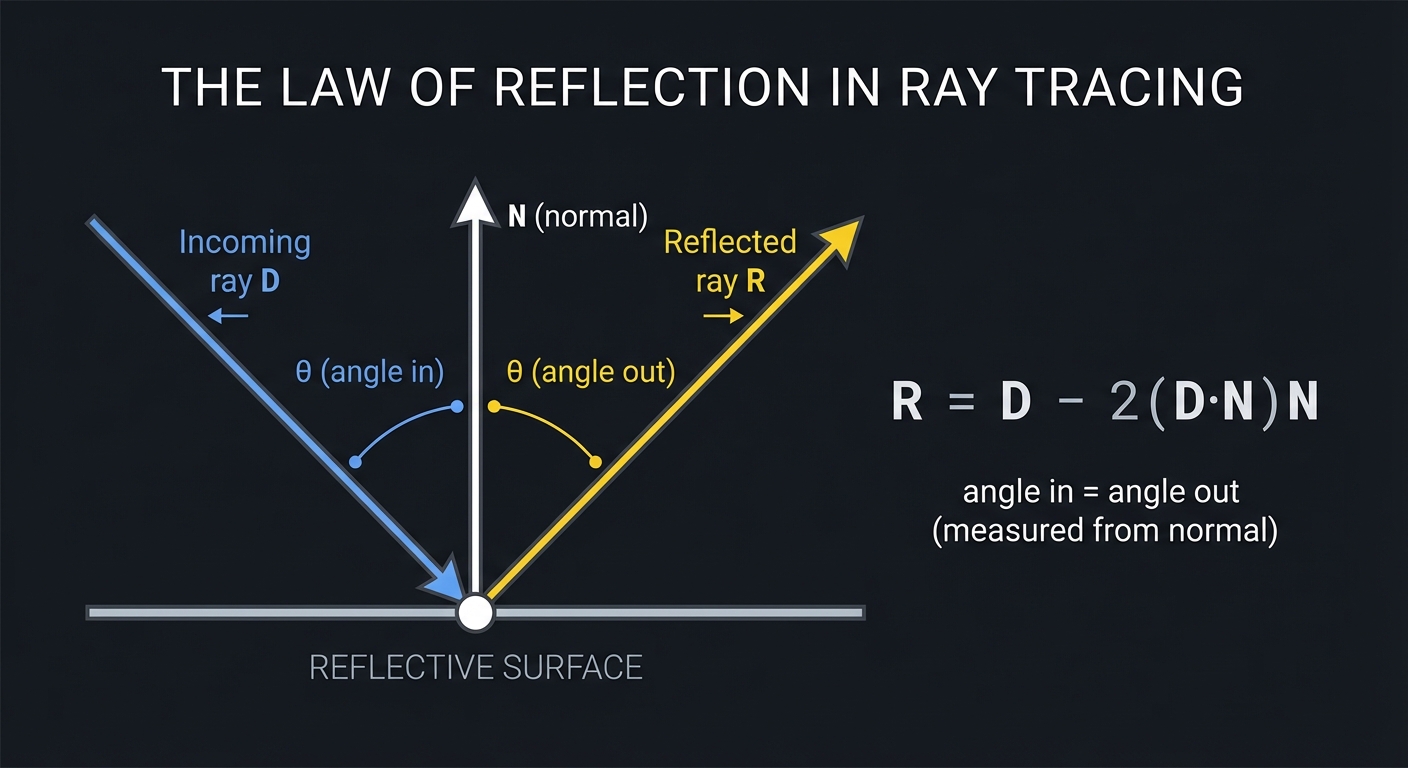
Recursively trace the reflected ray:
def trace(ray, depth):
if depth > MAX_DEPTH:
return BLACK
hit = find_closest_intersection(ray)
if not hit:
return BACKGROUND_COLOR
color = compute_lighting(hit)
if material.reflective > 0:
reflect_dir = reflect(ray.direction, hit.normal)
reflect_ray = Ray(hit.point + EPSILON * reflect_dir, reflect_dir)
color += material.reflective * trace(reflect_ray, depth + 1)
return color
Refraction (Glass, Water)
For transparent objects, rays bend according to Snellโs law:
nโ sin(ฮธโ) = nโ sin(ฮธโ)
Where:
- nโ = refractive index of material ray is leaving
- nโ = refractive index of material ray is entering
- ฮธโ = incident angle (from normal)
- ฮธโ = refracted angle
Air: n โ 1.0
Water: n โ 1.33
Glass: n โ 1.5
Diamond: n โ 2.4
Vector form of refraction:
ฮท = nโ/nโ (ratio of refractive indices)
c = -N ยท I (cosine of incident angle, I is incoming direction)
T = ฮท ร I + (ฮท ร c - โ(1 - ฮทยฒ(1 - cยฒ))) ร N
Where T is the transmitted (refracted) direction.
Total Internal Reflection: When going from dense to less dense medium at steep angles:
If 1 - ฮทยฒ(1 - cยฒ) < 0:
No refraction possible โ perfect reflection instead
Part 6: Camera and View Transformations
Camera Model
The camera defines our viewpoint:
Camera parameters:
- Position (eye): where camera is located
- Look-at (target): what it's pointing at
- Up vector: which way is "up"
- Field of view (FOV): how wide the view is
- Aspect ratio: width/height of image
Generating Primary Rays
For each pixel, generate a ray from camera through that pixel:
1. Compute camera coordinate system:
forward = normalize(target - eye)
right = normalize(forward ร up)
camera_up = right ร forward
2. Compute image plane dimensions:
half_height = tan(FOV/2)
half_width = half_height ร aspect_ratio
3. For pixel (x, y) in image of size (width, height):
u = (2 ร (x + 0.5) / width - 1) ร half_width
v = (1 - 2 ร (y + 0.5) / height) ร half_height
direction = normalize(forward + u ร right + v ร camera_up)
ray = Ray(eye, direction)
View Matrix (Connection to P01)
This is the same view matrix from P01:
View matrix converts world coordinates to camera coordinates.
For ray tracing, we go the opposite direction:
Convert screen coordinates to world rays.
Part 7: Object Transformations
Transforming Objects
Instead of transforming every point of an object, transform the ray:
To intersect ray with transformed object:
1. Transform ray INTO object's local space (inverse transform)
2. Intersect with untransformed object
3. Transform hit point and normal BACK to world space
This is more efficient than transforming every vertex!
For object with transformation matrix M:
World ray: R(t) = O_world + t ร D_world
Local ray: R(t) = MโปยนO_world + t ร MโปยนD_world
Note: MโปยนD doesn't need translation part (directions, not points)
After intersection at local point P_local with normal N_local:
P_world = M ร P_local
N_world = normalize(transpose(Mโปยน) ร N_local)
The normal transforms with the inverse-transpose!
This uses matrix inverses extensively!
Part 8: Global Illumination
Beyond Direct Lighting
Direct lighting only considers paths: Camera โ Surface โ Light
Global illumination considers all light paths, including:
- Camera โ Surface โ Surface โ Light (indirect lighting)
- Camera โ Surface โ Surface โ โฆ โ Light (multiple bounces)
This creates:
- Color bleeding (red wall tints white floor pink)
- Soft indirect shadows
- Realistic ambient light
Monte Carlo Path Tracing
Sample random light paths:
def path_trace(ray, depth):
if depth > MAX_DEPTH:
return BLACK
hit = find_intersection(ray)
if not hit:
return BACKGROUND
# Emitted light (if hit a light source)
color = hit.material.emission
# Sample a random direction for next bounce
new_dir = sample_hemisphere(hit.normal)
new_ray = Ray(hit.point + EPSILON * new_dir, new_dir)
# Recursive call (the next bounce)
incoming = path_trace(new_ray, depth + 1)
# BRDF: how much incoming light is reflected toward camera
brdf = hit.material.color / PI # Lambertian diffuse
cos_theta = dot(new_dir, hit.normal)
color += brdf * incoming * cos_theta * 2 * PI # PDF = 1/(2ฯ)
return color
Importance Sampling
Donโt sample uniformly โ sample more in directions that contribute more:
Cosine-weighted hemisphere sampling:
- Sample more in directions aligned with normal
- Fewer wasted samples pointing along the surface
Light importance sampling:
- Sample more toward bright light sources
- Converges faster for scenes with small bright lights
Building Orthonormal Bases
To sample a hemisphere around the normal, build a local coordinate system:
def build_onb(n):
"""Build orthonormal basis from normal n."""
# Find a non-parallel vector
if abs(n.x) > 0.9:
a = Vec3(0, 1, 0)
else:
a = Vec3(1, 0, 0)
# Build perpendicular vectors
t = normalize(cross(n, a)) # tangent
b = cross(n, t) # bitangent
return (t, b, n)
def sample_hemisphere(normal):
"""Sample random direction in hemisphere around normal."""
t, b, n = build_onb(normal)
# Random point on unit hemisphere (cosine-weighted)
r1 = random()
r2 = random()
sin_theta = sqrt(r1)
cos_theta = sqrt(1 - r1)
phi = 2 * PI * r2
# Convert to cartesian (local coordinates)
x = sin_theta * cos(phi)
y = sin_theta * sin(phi)
z = cos_theta
# Transform to world coordinates
return x * t + y * b + z * n
This constructs an orthonormal basis using cross products!
Part 9: Putting It All Together
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ COMPLETE RAY TRACING PIPELINE โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโค
โ โ
โ For each pixel (x, y): โ
โ โโโโโโโโโโโโโโโโโโโโโโ โ
โ โ
โ โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ 1. GENERATE PRIMARY RAY โ โ
โ โ direction = camera_forward + u ร right + v ร up โ โ
โ โ ray = Ray(camera_position, normalize(direction)) โ โ
โ โ โ โ
โ โ LINEAR ALGEBRA: orthonormal basis, normalization โ โ
โ โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโฌโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ
โ โผ โ
โ โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ 2. FIND CLOSEST INTERSECTION โ โ
โ โ For each object: โ โ
โ โ If transformed: ray_local = inverse(M) ร ray_world โ โ
โ โ Solve intersection equations โ โ
โ โ Keep closest positive t โ โ
โ โ โ โ
โ โ LINEAR ALGEBRA: matrix inverse, quadratic/linear equations โ โ
โ โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโฌโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ
โ hit found? โ โ
โ โโโโโ no โโโโโโโผโโโโโ yes โโโโโ โ
โ โ โ โ โ
โ โผ โ โผ โ
โ [return sky] โ โโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ 3. COMPUTE NORMAL โ โ
โ โ โ N = normalize(P - C) โ โ
โ โ โ (for sphere) โ โ
โ โ โ N = (B-A) ร (C-A) โ โ
โ โ โ (for triangle) โ โ
โ โ โ โ โ
โ โ โ LINEAR ALGEBRA: cross, โ โ
โ โ โ normalize โ โ
โ โ โโโโโโโโโโโโโฌโโโโโโโโโโโโโ โ
โ โ โ โ
โ โ โผ โ
โ โ โโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ 4. COMPUTE LIGHTING โ โ
โ โ โ For each light: โ โ
โ โ โ L = normalize( โ โ
โ โ โ light_pos - P) โ โ
โ โ โ diffuse = max(0, โ โ
โ โ โ N ยท L) โ โ
โ โ โ shadow_ray check โ โ
โ โ โ โ โ
โ โ โ LINEAR ALGEBRA: dot โ โ
โ โ โ product = cosine angle โ โ
โ โ โโโโโโโโโโโโโฌโโโโโโโโโโโโโ โ
โ โ โ โ
โ โ โผ โ
โ โ โโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ 5. REFLECTION/REFRACTIONโ โ
โ โ โ R = D - 2(DยทN)N โ โ
โ โ โ Trace reflected ray โ โ
โ โ โ (recursive call) โ โ
โ โ โ โ โ
โ โ โ LINEAR ALGEBRA: vector โ โ
โ โ โ reflection formula โ โ
โ โ โโโโโโโโโโโโโฌโโโโโโโโโโโโโ โ
โ โ โ โ
โ โ โผ โ
โ โ โโโโโโโโโโโโโโโโโโโโโโโโโโ โ
โ โ โ 6. COMBINE COLORS โ โ
โ โ โ return ambient + โ โ
โ โ โ diffuse + specular + โ โ
โ โ โ reflection + refract โ โ
โ โ โโโโโโโโโโโโโฌโโโโโโโโโโโโโ โ
โ โ โ โ
โ โโโโโโโโโโโโโโโโโ โ
โ โ
โ Store color in image[x][y] โ
โ โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
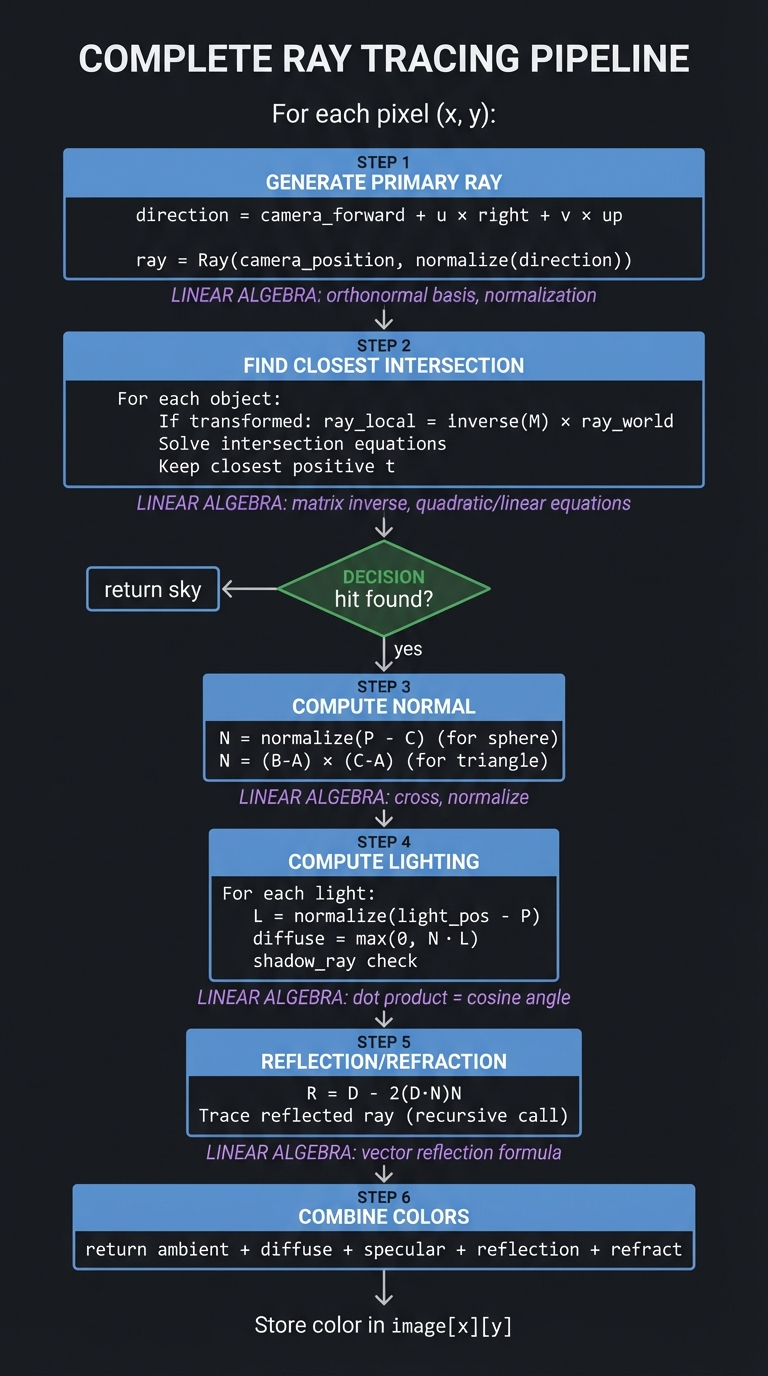
Project Specification
What Youโre Building
A ray tracer that:
- Renders 3D scenes with spheres, planes, and triangles
- Computes shadows from point lights
- Handles reflective surfaces (mirrors)
- Handles refractive surfaces (glass)
- Outputs images to file (PPM, PNG)
Minimum Requirements
- Ray-sphere intersection
- Ray-plane intersection
- Phong lighting (ambient + diffuse + specular)
- Hard shadows
- Reflections (recursive ray tracing)
- Camera positioning
- Output image to file
Stretch Goals
- Ray-triangle intersection (mesh rendering)
- Refraction with Fresnel effect
- Texture mapping
- Area lights and soft shadows
- Monte Carlo path tracing
- BVH acceleration structure
- Multithreading
Solution Architecture
Data Structures
typedef struct {
Vec3 origin;
Vec3 direction;
} Ray;
typedef struct {
Vec3 point;
Vec3 normal;
float t; // distance along ray
int object_index;
Vec2 uv; // texture coordinates
} HitRecord;
typedef struct {
Vec3 color;
float ambient;
float diffuse;
float specular;
float shininess;
float reflective;
float refractive;
float ior; // index of refraction
} Material;
typedef struct {
Vec3 center;
float radius;
Material material;
} Sphere;
typedef struct {
Vec3 point;
Vec3 normal;
Material material;
} Plane;
typedef struct {
Vec3 a, b, c;
Material material;
} Triangle;
typedef struct {
Vec3 position;
float fov;
Vec3 look_at;
Vec3 up;
} Camera;
typedef struct {
Vec3 position;
Vec3 color;
float intensity;
} Light;
typedef struct {
Sphere* spheres;
int num_spheres;
Plane* planes;
int num_planes;
Triangle* triangles;
int num_triangles;
Light* lights;
int num_lights;
Camera camera;
Vec3 background;
} Scene;
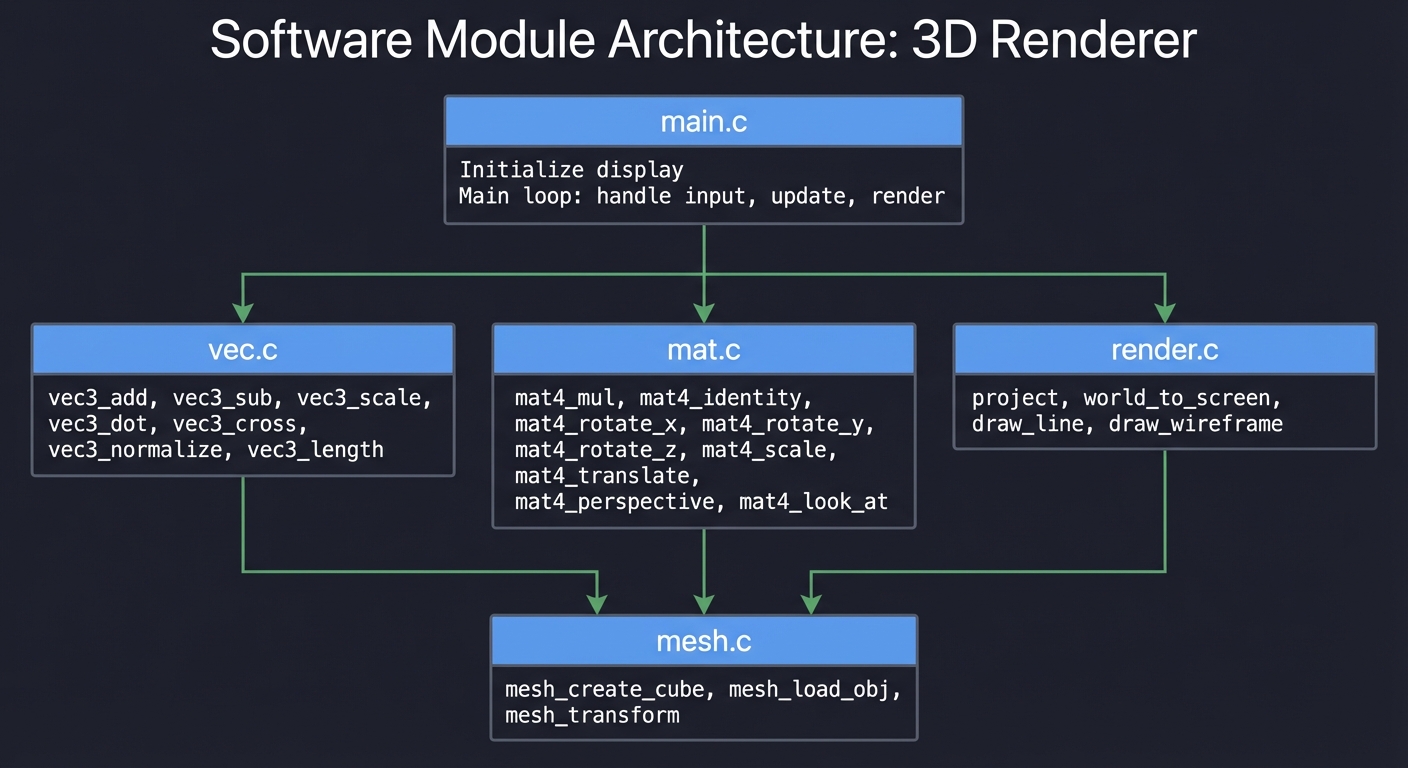
Module Structure
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ main.c โ
โ - Parse scene file or create scene โ
โ - Render loop: for each pixel, trace ray โ
โ - Write output image โ
โโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโโ
โ
โโโโโโโโโโโโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโโโโโโโโ
โผ โผ โผ
โโโโโโโโโโโโโโโโ โโโโโโโโโโโโโโโโ โโโโโโโโโโโโโโโโ
โ vec.c โ โ ray.c โ โ camera.c โ
โ โ โ โ โ โ
โ vec3_add โ โ ray_create โ โ camera_ray โ
โ vec3_sub โ โ ray_at โ โ build_frame โ
โ vec3_dot โ โ โ โ โ
โ vec3_cross โ โ โ โ โ
โ vec3_normalizeโ โ โ โ โ
โ vec3_reflect โ โ โ โ โ
โ vec3_refract โ โ โ โ โ
โโโโโโโโโโโโโโโโ โโโโโโโโโโโโโโโโ โโโโโโโโโโโโโโโโ
โ โ
โโโโโโโโโโโโโโโโโโโโโโโโผโโโโโโโโโโโโโโโโโโโโโโโ
โผ โผ
โโโโโโโโโโโโโโโโ โโโโโโโโโโโโโโโโ
โ intersect.c โ โ shade.c โ
โ โ โ โ
โ sphere_hit โ โ compute_colorโ
โ plane_hit โ โ phong_shade โ
โ triangle_hit โ โ shadow_ray โ
โ scene_hit โ โ reflect_ray โ
โโโโโโโโโโโโโโโโ โ refract_ray โ
โโโโโโโโโโโโโโโโ
โ
โผ
โโโโโโโโโโโโโโโโ
โ image.c โ
โ โ
โ image_create โ
โ image_write โ
โ gamma_correctโ
โโโโโโโโโโโโโโโโ
Phased Implementation Guide
Phase 1: Basic Infrastructure (Days 1-4)
Goal: Set up project structure and vector math
Tasks:
- Implement Vec3 with all operations
- Implement Ray structure
- Create basic image output (PPM format)
- Test with a simple gradient image
Implementation:
// vec.c
Vec3 vec3_add(Vec3 a, Vec3 b) {
return (Vec3){a.x + b.x, a.y + b.y, a.z + b.z};
}
Vec3 vec3_cross(Vec3 a, Vec3 b) {
return (Vec3){
a.y * b.z - a.z * b.y,
a.z * b.x - a.x * b.z,
a.x * b.y - a.y * b.x
};
}
Vec3 vec3_reflect(Vec3 v, Vec3 n) {
// R = v - 2(vยทn)n
float dn = 2.0f * vec3_dot(v, n);
return vec3_sub(v, vec3_scale(n, dn));
}
// image.c
void write_ppm(const char* filename, Vec3* pixels, int w, int h) {
FILE* f = fopen(filename, "w");
fprintf(f, "P3\n%d %d\n255\n", w, h);
for (int i = 0; i < w * h; i++) {
int r = (int)(255 * clamp(pixels[i].x, 0, 1));
int g = (int)(255 * clamp(pixels[i].y, 0, 1));
int b = (int)(255 * clamp(pixels[i].z, 0, 1));
fprintf(f, "%d %d %d\n", r, g, b);
}
fclose(f);
}
Phase 2: Ray Generation and Sphere Intersection (Days 5-9)
Goal: Cast rays and detect sphere hits
Tasks:
- Implement camera ray generation
- Implement ray-sphere intersection
- Render spheres with normal visualization
- Add multiple spheres
Implementation:
Ray camera_ray(Camera* cam, float u, float v) {
// Build camera coordinate frame
Vec3 w = vec3_normalize(vec3_sub(cam->position, cam->look_at));
Vec3 u_axis = vec3_normalize(vec3_cross(cam->up, w));
Vec3 v_axis = vec3_cross(w, u_axis);
float theta = cam->fov * M_PI / 180.0f;
float half_height = tan(theta / 2);
float half_width = half_height * cam->aspect;
Vec3 lower_left = vec3_sub(
vec3_sub(cam->position, vec3_scale(u_axis, half_width)),
vec3_add(vec3_scale(v_axis, half_height), w)
);
Vec3 horizontal = vec3_scale(u_axis, 2 * half_width);
Vec3 vertical = vec3_scale(v_axis, 2 * half_height);
Vec3 direction = vec3_add(
vec3_add(lower_left, vec3_scale(horizontal, u)),
vec3_sub(vec3_scale(vertical, v), cam->position)
);
return (Ray){cam->position, vec3_normalize(direction)};
}
bool sphere_hit(Sphere* s, Ray* r, float t_min, float t_max, HitRecord* rec) {
Vec3 oc = vec3_sub(r->origin, s->center);
float a = vec3_dot(r->direction, r->direction);
float b = vec3_dot(oc, r->direction);
float c = vec3_dot(oc, oc) - s->radius * s->radius;
float discriminant = b*b - a*c;
if (discriminant < 0) return false;
float sqrt_d = sqrt(discriminant);
float t = (-b - sqrt_d) / a;
if (t < t_min || t > t_max) {
t = (-b + sqrt_d) / a;
if (t < t_min || t > t_max) return false;
}
rec->t = t;
rec->point = ray_at(r, t);
rec->normal = vec3_scale(vec3_sub(rec->point, s->center), 1.0f / s->radius);
return true;
}
Phase 3: Lighting and Shadows (Days 10-14)
Goal: Add realistic lighting
Tasks:
- Implement Phong shading model
- Add point lights
- Implement shadow rays
- Handle multiple lights
Implementation:
Vec3 shade(Scene* scene, Ray* ray, HitRecord* hit, Material* mat) {
Vec3 color = vec3_scale(mat->color, mat->ambient);
for (int i = 0; i < scene->num_lights; i++) {
Light* light = &scene->lights[i];
// Direction to light
Vec3 L = vec3_normalize(vec3_sub(light->position, hit->point));
// Shadow ray
Ray shadow_ray = {
vec3_add(hit->point, vec3_scale(hit->normal, 0.001f)),
L
};
float light_dist = vec3_length(vec3_sub(light->position, hit->point));
HitRecord shadow_hit;
if (scene_hit(scene, &shadow_ray, 0.001f, light_dist, &shadow_hit)) {
continue; // In shadow
}
// Diffuse
float diff = fmax(0, vec3_dot(hit->normal, L));
color = vec3_add(color, vec3_scale(
vec3_mul(mat->color, light->color),
diff * mat->diffuse * light->intensity
));
// Specular
Vec3 V = vec3_scale(ray->direction, -1);
Vec3 R = vec3_reflect(vec3_scale(L, -1), hit->normal);
float spec = pow(fmax(0, vec3_dot(R, V)), mat->shininess);
color = vec3_add(color, vec3_scale(
light->color,
spec * mat->specular * light->intensity
));
}
return color;
}
Phase 4: Reflections (Days 15-19)
Goal: Add mirror reflections
Tasks:
- Implement recursive ray tracing
- Add reflection coefficient to materials
- Handle maximum recursion depth
- Test with mirror spheres
Implementation:
Vec3 trace(Scene* scene, Ray* ray, int depth) {
if (depth <= 0) return scene->background;
HitRecord hit;
if (!scene_hit(scene, ray, 0.001f, INFINITY, &hit)) {
return scene->background;
}
Material* mat = get_material(scene, hit.object_index);
Vec3 color = shade(scene, ray, &hit, mat);
// Reflection
if (mat->reflective > 0 && depth > 0) {
Vec3 reflect_dir = vec3_reflect(ray->direction, hit.normal);
Ray reflect_ray = {
vec3_add(hit.point, vec3_scale(hit.normal, 0.001f)),
reflect_dir
};
Vec3 reflect_color = trace(scene, &reflect_ray, depth - 1);
color = vec3_add(
vec3_scale(color, 1 - mat->reflective),
vec3_scale(reflect_color, mat->reflective)
);
}
return color;
}
Phase 5: Refraction (Days 20-25)
Goal: Add glass/water effects
Tasks:
- Implement Snellโs law vector form
- Handle total internal reflection
- Implement Fresnel equations (or approximation)
- Test with glass spheres
Implementation:
bool refract(Vec3 v, Vec3 n, float ni_over_nt, Vec3* refracted) {
Vec3 uv = vec3_normalize(v);
float dt = vec3_dot(uv, n);
float discriminant = 1.0f - ni_over_nt * ni_over_nt * (1 - dt*dt);
if (discriminant > 0) {
*refracted = vec3_sub(
vec3_scale(vec3_sub(uv, vec3_scale(n, dt)), ni_over_nt),
vec3_scale(n, sqrt(discriminant))
);
return true;
}
return false; // Total internal reflection
}
float schlick(float cosine, float ior) {
// Schlick's approximation for Fresnel
float r0 = (1 - ior) / (1 + ior);
r0 = r0 * r0;
return r0 + (1 - r0) * pow(1 - cosine, 5);
}
Phase 6: More Geometry (Days 26-30)
Goal: Add planes and triangles
Tasks:
- Implement ray-plane intersection
- Implement ray-triangle intersection
- Add floor/walls to scenes
- Load simple OBJ meshes
Implementation:
bool plane_hit(Plane* p, Ray* r, float t_min, float t_max, HitRecord* rec) {
float denom = vec3_dot(r->direction, p->normal);
if (fabs(denom) < 0.0001f) return false;
float t = vec3_dot(vec3_sub(p->point, r->origin), p->normal) / denom;
if (t < t_min || t > t_max) return false;
rec->t = t;
rec->point = ray_at(r, t);
rec->normal = p->normal;
return true;
}
bool triangle_hit(Triangle* tri, Ray* r, float t_min, float t_max, HitRecord* rec) {
// Mรถller-Trumbore algorithm
Vec3 edge1 = vec3_sub(tri->b, tri->a);
Vec3 edge2 = vec3_sub(tri->c, tri->a);
Vec3 h = vec3_cross(r->direction, edge2);
float a = vec3_dot(edge1, h);
if (fabs(a) < 0.0001f) return false;
float f = 1.0f / a;
Vec3 s = vec3_sub(r->origin, tri->a);
float u = f * vec3_dot(s, h);
if (u < 0 || u > 1) return false;
Vec3 q = vec3_cross(s, edge1);
float v = f * vec3_dot(r->direction, q);
if (v < 0 || u + v > 1) return false;
float t = f * vec3_dot(edge2, q);
if (t < t_min || t > t_max) return false;
rec->t = t;
rec->point = ray_at(r, t);
rec->normal = vec3_normalize(vec3_cross(edge1, edge2));
return true;
}
Phase 7: Path Tracing and Global Illumination (Days 31-40)
Goal: Add physically-based rendering
Tasks:
- Implement hemisphere sampling
- Add Monte Carlo integration
- Implement importance sampling
- Multiple samples per pixel
Phase 8: Optimization (Days 41-50)
Goal: Make it fast
Tasks:
- Add bounding volume hierarchy (BVH)
- Implement multithreading
- Add antialiasing
- Profile and optimize hot paths
Testing Strategy
Unit Tests
- Vector operations:
- Reflection formula: reflect([1,1,0], [0,1,0]) = [1,-1,0]
- Refraction at 45ยฐ through glass
- Cross product orthogonality
- Intersections:
- Ray through sphere center hits at expected t
- Ray tangent to sphere has one intersection
- Ray missing sphere returns false
- Lighting:
- Surface facing light is bright
- Surface facing away is dark
- Point in shadow receives no diffuse
Visual Tests
- Sphere shading: Should show smooth shading with highlight
- Reflections: Should show correct reflected scene
- Shadows: Sharp edges from point lights
- Refraction: Glass ball should invert/distort background
Reference Comparisons
Compare your output to:
- Ray tracing tutorials (Scratchapixel, Ray Tracing in One Weekend)
- Reference implementations
- Offline renders from Blender/PBRT
Common Pitfalls and Debugging
Shadow Acne
Symptom: Random dark spots on surfaces
Cause: Shadow ray starts inside surface due to floating-point error
Fix: Offset shadow ray origin by small epsilon along normal
Reflection Artifacts
Symptom: Incorrect reflections or black spots
Cause: Reflected ray direction not normalized, or wrong sign
Fix: Verify reflection formula: R = D - 2(DยทN)N
Inside-Out Normals
Symptom: Surfaces appear dark or lit from wrong side
Cause: Normal pointing wrong direction
Fix: Flip normal if dot(ray_direction, normal) > 0
Refraction Index Flip
Symptom: Glass looks wrong, total internal reflection in wrong places
Cause: Confusion about which medium ray is in
Fix: Track inside/outside state, flip normal and IOR accordingly
Numerical Precision
Symptom: Visual artifacts at edges, noise
Cause: Floating-point precision issues
Fix: Use appropriate epsilon values, avoid dividing by very small numbers
Extensions and Challenges
Beginner Extensions
- More primitive types (box, cylinder, cone)
- Multiple materials (metal, plastic, matte)
- Scene file loading (JSON/YAML)
Intermediate Extensions
- Texture mapping (image textures)
- Normal mapping
- Area lights
- Depth of field (thin lens camera)
Advanced Extensions
- Bidirectional path tracing
- Metropolis light transport
- Subsurface scattering
- Volumetric rendering (fog, clouds)
Real-World Connections
Film and Visual Effects
Pixarโs RenderMan, Disneyโs Hyperion, Wetaโs Manuka โ all path tracers:
- Every Pixar movie since Monsters University uses path tracing
- Complex materials, global illumination, photorealism
Video Games
Real-time ray tracing in modern GPUs:
- NVIDIA RTX, AMD RDNA2
- Reflections, shadows, global illumination
- Same math, specialized hardware
Architecture and Product Design
Accurate visualization before building:
- Architectural renders
- Automotive design
- Product photography replacement
Scientific Visualization
Rendering physical simulations:
- Medical imaging
- Molecular visualization
- Astrophysics simulation
Self-Assessment Checklist
Conceptual Understanding
- I can derive the ray-sphere intersection formula
- I understand why the dot product computes lighting
- I can explain the reflection formula geometrically
- I understand Snellโs law and total internal reflection
- I can explain how path tracing achieves global illumination
Practical Skills
- I implemented ray-sphere, ray-plane, and ray-triangle intersection
- My renders show correct shadows
- Reflections work recursively
- Refraction handles glass correctly
- I can render complex scenes
Teaching Test
Can you explain to someone else:
- How do you find where a ray hits a sphere?
- Why does the dot product compute lighting intensity?
- How does recursive ray tracing create reflections?
- What makes path tracing physically accurate?
Resources
Primary
- โRay Tracing in One Weekendโ by Peter Shirley (free online)
- โComputer Graphics from Scratchโ by Gabriel Gambetta
- โPhysically Based Renderingโ by Pharr, Jakob, Humphreys
Reference
- Scratchapixel (scratchapixel.com) - Detailed tutorials
- PBRT source code - Production-quality reference
- โReal-Time Renderingโ - Advanced techniques
Tools
- Blender - For creating test scenes
- Intel Embree - Optimized ray tracing kernels
- NVIDIA OptiX - GPU ray tracing
Conclusion
When you complete this capstone, you will have built a photorealistic rendering engine using nothing but linear algebra. Every concept from the previous projects comes together:
- Vectors from P01 become rays and directions
- Matrices from P01 transform objects and cameras
- Decomposition concepts from P02 appear in importance sampling
- Optimization from P03 applies to rendering performance
- Equation solving from P04 handles intersections
- Similarity measures from P05 apply to material BRDFs
You will have proven, irrefutably, that you understand linear algebraโbecause you used it to simulate physics accurately enough to create images indistinguishable from reality.
This is the ultimate demonstration of linear algebra mastery: turning mathematical abstractions into visual beauty.