P01: Universal Number Base Converter
The Core Question: “How does the computer understand that the symbols ‘255’, ‘FF’, and ‘11111111’ all represent the same value?”
Learning Objectives
By completing this project, you will:
- Master positional notation - Understand that every number system works the same way, just with different bases
- Implement the division-remainder algorithm - Convert from decimal to any base without using built-in functions
- Implement the power-summation algorithm - Convert from any base to decimal manually
- Internalize the binary-hex relationship - Instantly recognize that 4 binary bits equal 1 hex digit
- Build professional CLI tools - Create a complete, validated, user-friendly command-line application
- Think like a computer - See numbers as abstract values with multiple representations
- Handle edge cases gracefully - Build robust software that fails gracefully with meaningful errors
Project Overview
| Attribute | Value |
|---|---|
| Main Language | Python |
| Alternative Languages | JavaScript (Node.js), Go, C# |
| Difficulty | Beginner |
| Time Estimate | Weekend (6-10 hours) |
| Prerequisites | Basic programming (loops, functions, conditionals) |
| Main Book | “Code: The Hidden Language” by Charles Petzold |
What You’ll Build
A command-line tool that converts numbers between decimal, binary, and hexadecimal. The tool accepts a number in any base, validates it, and outputs the equivalent representation in the target base.
Example usage:
$ python converter.py --from dec --to hex 255
FF
$ python converter.py --from bin --to dec 11111111
255
$ python converter.py --from hex --to bin FF
11111111
The key constraint: You must implement the conversion algorithms yourself. Do not use Python’s bin(), hex(), or int(x, base) functions. The learning happens when you write the logic.
Real World Outcome
When you complete this project, you’ll have a professional utility you can use whenever you need quick conversions. Here’s exactly what your tool will produce:
Example 1: Decimal to Hexadecimal Conversion
$ python converter.py --from dec --to hex 255
Input: 255 (decimal)
Binary: 11111111
Hex: FF
Output: FF (hexadecimal)
Example 2: Hexadecimal to Decimal (Memory Addresses)
$ python converter.py --from hex --to dec 0x7FFF5C2A
Input: 0x7FFF5C2A (hexadecimal)
Decimal: 2147466282
Binary: 01111111111111110101110000101010
Output: 2147466282 (decimal)
Example 3: Binary to All Formats
$ python converter.py --from bin --to all 11010110
Input: 11010110 (binary)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Decimal: 214
Hex: D6
Octal: 326
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
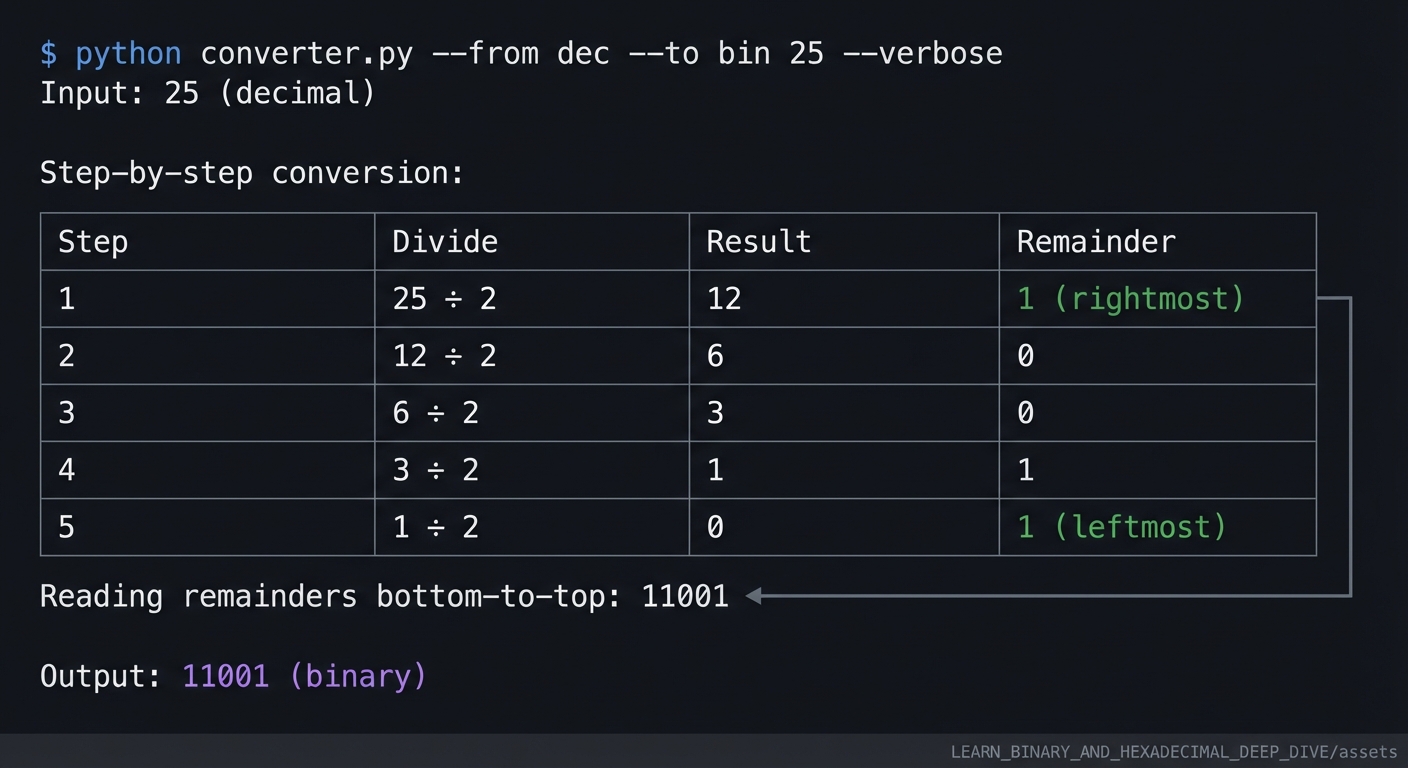
Example 4: Verbose Mode (Shows Work)
$ python converter.py --from dec --to bin 25 --verbose
Input: 25 (decimal)
Step-by-step conversion:
┌──────┬────────┬────────┬───────────────┐
│ Step │ Divide │ Result │ Remainder │
├──────┼────────┼────────┼───────────────┤
│ 1 │ 25 ÷ 2 │ 12 │ 1 (rightmost) │
│ 2 │ 12 ÷ 2 │ 6 │ 0 │
│ 3 │ 6 ÷ 2 │ 3 │ 0 │
│ 4 │ 3 ÷ 2 │ 1 │ 1 │
│ 5 │ 1 ÷ 2 │ 0 │ 1 (leftmost) │
└──────┴────────┴────────┴───────────────┘
Reading remainders bottom-to-top: 11001
Output: 11001 (binary)
Example 5: Batch Processing Mode
$ python converter.py --batch conversions.txt
Processing 5 conversions...
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
[1] 127 (dec) → 0x7F (hex)
[2] 0xFF (hex) → 255 (dec)
[3] 10101010 (bin) → 170 (dec)
[4] 256 (dec) → 100000000 (bin)
[5] CAFE (hex) → 51966 (dec)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
All conversions complete.
Example 6: Error Handling
$ python converter.py --from hex --to dec "GG"
Error: Invalid hexadecimal input 'GG'
Hexadecimal digits must be 0-9 or A-F.
$ python converter.py --from bin --to dec "12345"
Error: Invalid binary input '12345'
Binary digits must be 0 or 1 only.
$ python converter.py --from dec --to hex -5
Error: Negative numbers not supported in this version.
Use unsigned integers only.
Real-World Scenarios Where You’ll Use This
After completing this project, you’ll use your converter for:
- Debugging memory dumps - Reading hex addresses from debuggers like lldb or gdb
- Understanding file permissions - Unix permissions like 0755 become readable
- Network programming - IP addresses and subnet masks in binary/hex
- Color values - Converting RGB decimal values to hex for CSS
- Reading assembly output - Understanding hex opcodes and addresses
- Cryptography work - Hash values and keys displayed in hexadecimal
The Core Question You’re Answering
“How does the computer understand that the symbols ‘255’, ‘FF’, and ‘11111111’ all represent the same value?”
This project answers the fundamental question that underlies all of computing. Here’s the deep insight:
Numbers Are Abstract; Notation Is Concrete
The value “two hundred fifty-five” exists as an abstract concept - the quantity of items in a set. When we write it down, we’re using a notation system to represent that abstract value:
┌─────────────────────────────────────────────────────────────────┐
│ THE SAME VALUE │
│ │
│ Decimal: 255 = 2×10² + 5×10¹ + 5×10⁰ │
│ = 200 + 50 + 5 │
│ │
│ Binary: 11111111 = 1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ │
│ + 1×2³ + 1×2² + 1×2¹ + 1×2⁰ │
│ = 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 │
│ │
│ Hexadecimal: FF = 15×16¹ + 15×16⁰ │
│ = 240 + 15 │
│ │
│ All equal: 255 │
└─────────────────────────────────────────────────────────────────┘

Why Different Bases Exist
- Decimal (Base 10): Humans have 10 fingers. We naturally count in tens.
- Binary (Base 2): Transistors have two states: ON (1) and OFF (0). Computers must use binary.
- Hexadecimal (Base 16): Perfect bridge between human readability and binary. 4 binary bits = 1 hex digit exactly.
The Magic Relationship: 4 Bits = 1 Hex Digit
This is the most important pattern to internalize:
Binary → Hex Mapping (Memorize This!)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
0000 = 0 0100 = 4 1000 = 8 1100 = C
0001 = 1 0101 = 5 1001 = 9 1101 = D
0010 = 2 0110 = 6 1010 = A 1110 = E
0011 = 3 0111 = 7 1011 = B 1111 = F
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Example:
Binary: 1010 0101
↓ ↓
Hex: A 5
Result: 0xA5
Reverse:
Hex: F 8
↓ ↓
Binary: 1111 1000
By building this converter from scratch, you prove to yourself that you understand the mechanics of positional number systems at a fundamental level.
Concepts You Must Understand First
Before writing any code, you need to internalize these prerequisite concepts. Do not skip this section - the depth of your understanding here determines your success.
1. Positional Notation (Place-Value System)
What it is: In any base-N system, each digit’s position represents a power of N. The rightmost position is N⁰ (always 1), then N¹, N², and so on moving left.
Book Reference: “Code: The Hidden Language of Computer Hardware and Software” by Charles Petzold, Chapter 7: “Counting”
ASCII Diagram - How Position Determines Value:
DECIMAL NUMBER: 1,234
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Position: 3 2 1 0
Power: 10³ 10² 10¹ 10⁰
Value: 1000 100 10 1
───── ───── ───── ─────
Digit: 1 2 3 4
───── ───── ───── ─────
Contribution: 1×1000 + 2×100 + 3×10 + 4×1
= 1000 + 200 + 30 + 4
= 1234
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
BINARY NUMBER: 1011
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Position: 3 2 1 0
Power: 2³ 2² 2¹ 2⁰
Value: 8 4 2 1
───── ───── ───── ─────
Digit: 1 0 1 1
───── ───── ───── ─────
Contribution: 1×8 + 0×4 + 1×2 + 1×1
= 8 + 0 + 2 + 1
= 11 (decimal)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
HEX NUMBER: 2F
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Position: 1 0
Power: 16¹ 16⁰
Value: 16 1
───── ─────
Digit: 2 F (=15)
───── ─────
Contribution: 2×16 + 15×1
= 32 + 15
= 47 (decimal)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
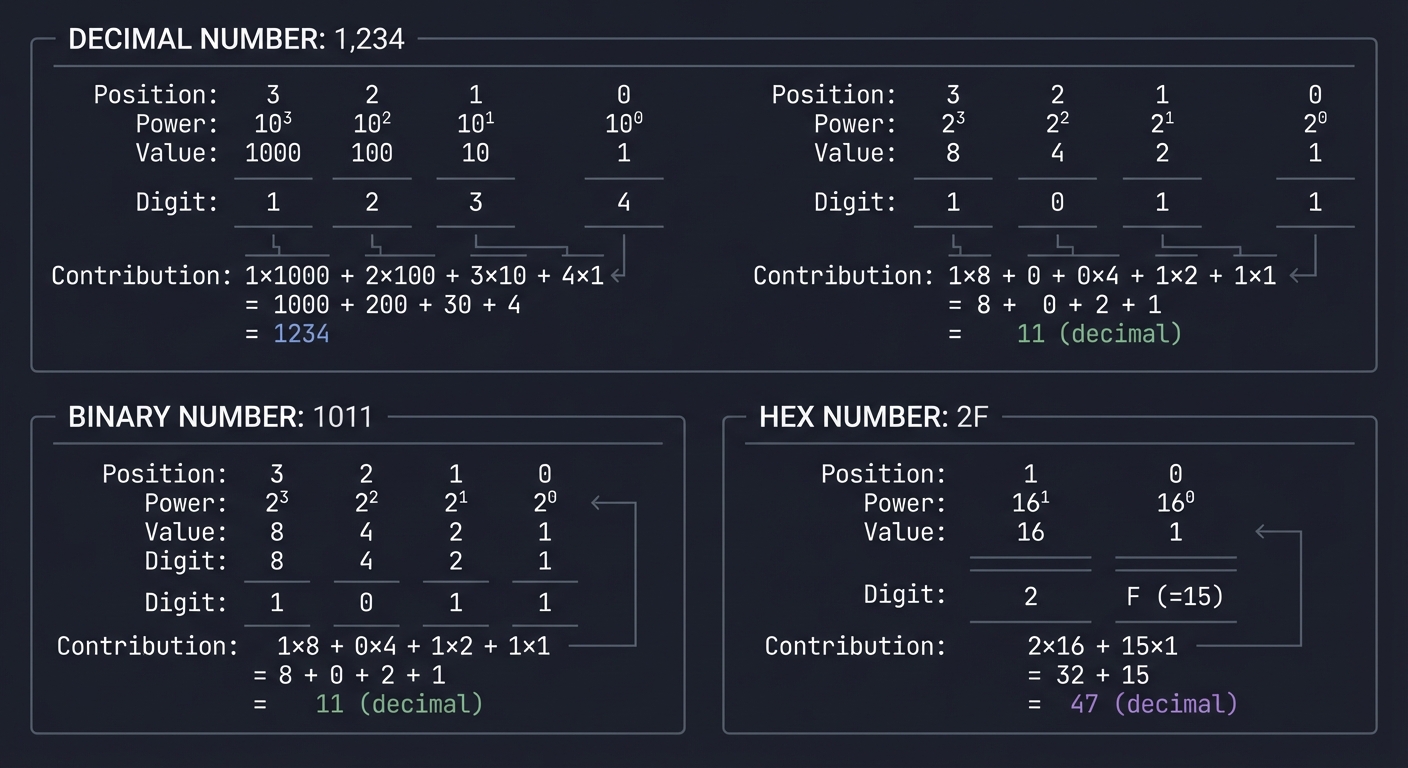
Why it matters: This is the entire mathematical foundation of base conversion. If you can apply this pattern, you can convert any base to decimal.
2. The Division-Remainder Algorithm
What it is: To convert from decimal to another base, repeatedly divide by the target base and collect the remainders. The remainders (read in reverse) form the digits of the result.
Book Reference: “Grokking Algorithms” by Aditya Bhargava, Chapter 1 - for understanding algorithmic thinking
Example - Convert Decimal 25 to Binary:
DECIMAL 25 TO BINARY
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Step 1: 25 ÷ 2 = 12 remainder 1 ← rightmost bit
Step 2: 12 ÷ 2 = 6 remainder 0
Step 3: 6 ÷ 2 = 3 remainder 0
Step 4: 3 ÷ 2 = 1 remainder 1
Step 5: 1 ÷ 2 = 0 remainder 1 ← leftmost bit
↑
STOP when quotient = 0
Read remainders BOTTOM to TOP: 11001
Verification: 1×16 + 1×8 + 0×4 + 0×2 + 1×1 = 25 ✓
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Example - Convert Decimal 255 to Hexadecimal:
DECIMAL 255 TO HEX
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Step 1: 255 ÷ 16 = 15 remainder 15 (=F) ← rightmost
Step 2: 15 ÷ 16 = 0 remainder 15 (=F) ← leftmost
↑
STOP when quotient = 0
Read remainders BOTTOM to TOP: FF
Verification: 15×16 + 15×1 = 240 + 15 = 255 ✓
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Why it matters: This algorithm is exactly what you’ll implement in code. You need to understand why it works mathematically.
3. String Manipulation
What it is: Numbers aren’t stored as strings, but user input comes as strings, and output goes as strings. You must know how to:
- Iterate through characters in a string
- Convert a character to its numeric value (‘7’ -> 7, ‘A’ -> 10)
- Build up a string character by character
- Reverse a string
Book Reference:
- Python: “Automate the Boring Stuff with Python” by Al Sweigart, Chapter 6
- JavaScript: “Eloquent JavaScript” by Marijn Haverbeke, Chapter 4
Example - Character to Value Conversion:
# How would you convert the string "A5" (hex) to decimal?
# Step 1: Split into characters
characters = ['A', '5']
# Step 2: Convert to numeric values
# 'A' -> 10 (because A is the 10th value after 0-9)
# '5' -> 5
values = [10, 5]
# Step 3: Apply positional math (base 16)
# 10 × 16¹ + 5 × 16⁰
# = 160 + 5
# = 165
# The conversion logic:
def hex_char_to_value(char):
if char.isdigit():
return int(char) # '5' -> 5
else:
return ord(char.upper()) - ord('A') + 10 # 'A' -> 10, 'B' -> 11, ...
Why it matters: Your entire converter is about transforming string representations of numbers. This is 50% of your implementation.
4. Command-Line Argument Parsing
What it is: Accepting input from the user when they run your program from the terminal.
Book Reference: Python official argparse module documentation
Example:
# The user types:
python converter.py --from hex --to dec FF
# Your program needs to extract:
# from_base = "hex"
# to_base = "dec"
# value = "FF"
Why it matters: A tool that requires code editing to change inputs isn’t a tool - it’s a code snippet. Proper CLI handling makes this professional.
5. Integer Division vs Float Division
What it is: The difference between operations that preserve the decimal part and those that truncate it.
Critical for Python:
# Float division (NOT what you want)
25 / 2 # = 12.5
# Integer division (WHAT you need)
25 // 2 # = 12
# Modulo (the remainder)
25 % 2 # = 1
Why it matters: When you divide 25 by 2, you need the result to be 12 (quotient) and 1 (remainder), not 12.5.
Language-specific notes:
| Language | Integer Division | Remainder |
|---|---|---|
| Python | x // y |
x % y |
| JavaScript | Math.floor(x/y) |
x % y |
| C/Go | x / y (for integers) |
x % y |
Questions to Guide Your Design
Before you write a single line of code, think through these design questions. Your answers will shape your implementation:
Input Handling Questions
- How will you handle different input formats?
- Will you accept
FF,0xFF,0XFF? What about lowercaseff? - Will you accept
11111111,0b11111111, or both? - Should leading zeros be preserved in output?
- Will you accept
- What about prefixes?
- Should hex require
0xor allow it optionally? - Should binary require
0b? - How do you distinguish between them for auto-detection?
- Should hex require
Validation Questions
- What validation will you implement?
- What happens if the user inputs
"123"but says it’s binary? - How will you handle negative numbers? (Two’s complement is complex)
- What’s the maximum number size you’ll support?
- What happens if the user inputs
- How will you report errors?
- Generic “Invalid input” or specific “Character ‘G’ is not valid in base 16”?
- Exit codes for scripting compatibility?
Architecture Questions
- How will you structure your conversion logic?
- Option A: Convert everything to decimal first, then to target base
- Option B: Direct binary<->hex using the nibble relationship
- Which is simpler? Which is more efficient?
- How will you organize your code?
- Suggested function structure:
parse_input(input_string, base)-> returns integer valueformat_output(number, base)-> returns string representationvalidate_input(input_string, base)-> returns (bool, error_message)main()-> orchestrates everything
- Suggested function structure:
Feature Scope Questions
- Should you handle floating-point numbers?
- Binary/hex floating-point (IEEE 754) is complex
- Integers-only is perfectly valid for v1.0
- Document this limitation for your users
- What output formats will you support?
- Just the raw number? (
FF) - With prefix? (
0xFF) - With explanation? (
FF (hexadecimal) = 255 (decimal)) - Verbose step-by-step?
- Just the raw number? (
Thinking Exercise
Before writing any code, complete these exercises on paper. This builds your intuition and makes the coding phase much easier.
Exercise 1: Manual Conversion Practice (30 minutes)
Convert these numbers by hand, showing all your work:
- Decimal 156 -> Binary
- Decimal 156 -> Hexadecimal
- Binary 10011101 -> Decimal
- Hexadecimal A7 -> Decimal
- Binary 11011010 -> Hexadecimal (use the nibble trick)
- Hexadecimal 3F -> Binary (use the nibble trick)
Check your work (scroll down):
Click to reveal answers
- 156 -> 10011100
- 156 -> 9C
- 10011101 -> 157
- A7 -> 167
- 11011010 -> DA
- 3F -> 00111111
Exercise 2: Algorithm Tracing (20 minutes)
Write out the division-remainder algorithm for converting decimal 89 to binary. Create this table:
| Step | Division | Quotient | Remainder |
|---|---|---|---|
| 1 | 89 / 2 | 44 | 1 |
| 2 | 44 / 2 | ? | ? |
| … | … | … | … |
Continue until the quotient reaches 0. Then read the remainders bottom-to-top.
Your answer: 89 decimal = ____ binary
Exercise 3: Edge Case Brainstorming (15 minutes)
List at least 10 potential edge cases or error conditions your program might encounter:
- Empty string input
- Input containing invalid characters for the specified base
- Input “0” (is the output “0” or “”?)
- Very large numbers that exceed your language’s integer size
- Negative numbers (do you support them?)
- Input with leading zeros (preserve them? strip them?)
- Input with spaces or special characters
- NULL/None/undefined input
- Base conversion to/from the same base (decimal to decimal)
- Mixed case input (0xFF vs 0xff vs 0xFf)
- Numbers with leading/trailing whitespace
- Unicode characters that look like digits
For each edge case, decide: crash, error message, or handle gracefully?
Exercise 4: Pseudocode First (45 minutes)
Write pseudocode (not real code) for your main conversion functions:
function decimal_to_any_base(decimal_number, target_base):
if decimal_number is 0:
return "0"
digits = empty list
while decimal_number > 0:
remainder = decimal_number modulo target_base
convert remainder to appropriate character (0-9 or A-F)
add character to beginning of digits list
decimal_number = decimal_number integer-divided-by target_base
return digits joined as string
Write similar pseudocode for:
any_base_to_decimal(input_string, source_base)validate_input(input_string, base)main_program_flow()
The Interview Questions They’ll Ask
If you truly understand this project, you should be able to answer these common interview questions confidently:
Basic Level
-
“How would you convert a decimal number to binary without using built-in functions?”
Expected answer: Use the division-remainder algorithm. Repeatedly divide by 2, collect remainders, reverse the result. Time complexity is O(log n) where n is the number.
-
“Why do we use hexadecimal in programming instead of binary?”
Expected answer: Hex is more compact and human-readable. One hex digit represents exactly 4 bits, making it a perfect shorthand for binary. The number 255 is
FFin hex vs11111111in binary. -
“What is the decimal value of the hexadecimal number 0xCAFE?”
Expected answer:
- C = 12, A = 10, F = 15, E = 14
- (12 x 16^3) + (10 x 16^2) + (15 x 16^1) + (14 x 16^0)
- = 49152 + 2560 + 240 + 14
- = 51,966
-
“What is 0xFF in decimal?”
Expected answer: 255. It’s the maximum value of an unsigned 8-bit integer.
Intermediate Level
-
“How would you implement a function to check if a string is a valid hexadecimal number?”
Expected answer: Iterate through each character and verify it’s in the set [0-9, A-F, a-f]. Optionally handle the ‘0x’ prefix. Use a regular expression for conciseness.
-
“What’s the difference between logical and arithmetic bit shifts?”
Expected answer: Logical shifts always fill with zeros. Arithmetic right shift preserves the sign bit (fills with copies of the MSB). This relates to signed vs unsigned integer representation.
-
“How is the number -1 represented in binary using two’s complement?”
Expected answer: In an 8-bit system, -1 is
11111111. In 16-bit, it’s1111111111111111. All bits are set to 1. (This extends beyond unsigned integers in your project.) -
“How would you convert between hex and binary without going through decimal?”
Expected answer: Use the nibble relationship. Group binary into 4-bit chunks and map each to a hex digit directly. This is O(n) where n is the number of digits.
Advanced Level
-
“How would you optimize base conversion for very large numbers (1000+ digits)?”
Expected answer: Use arbitrary-precision arithmetic (like Python’s built-in or GMP library). Consider divide-and-conquer algorithms. For converting between bases that are powers of 2, use bit manipulation directly.
-
“Explain how floating-point numbers are stored in binary (IEEE 754).”
Expected answer: Sign bit (1), exponent (8 or 11 bits), mantissa (23 or 52 bits). The exponent is biased. The mantissa has an implicit leading 1. Special values for infinity and NaN.
-
“If you’re debugging a network packet dump, you see ‘0x0A 0x00 0x00 0x01’. What might this represent?”
Expected answer: Could be an IPv4 address (10.0.0.1) in network byte order (big-endian). Shows ability to connect number systems to real protocols.
Behavioral/Design Questions
-
“Walk me through how you would design a command-line tool for base conversion.”
Expected answer: Requirements gathering, user interface design, error handling strategy, modular architecture, testing approach, documentation, and future extensibility.
-
“You discover your converter gives wrong results for numbers above 2^31. How do you debug this?”
Expected answer: Check for integer overflow, use larger integer types or arbitrary-precision libraries, add test cases for boundary values.
Implementation Milestones
Use these milestones to track your progress. Each milestone represents a meaningful checkpoint.
Milestone 1: Basic Decimal to Binary (1-2 hours)
Goal: Implement decimal_to_binary(n) that returns a binary string.
Test cases:
decimal_to_binary(0) -> "0"
decimal_to_binary(1) -> "1"
decimal_to_binary(2) -> "10"
decimal_to_binary(10) -> "1010"
decimal_to_binary(255) -> "11111111"
You understand: The division-remainder algorithm works.
Milestone 2: Binary to Decimal (1 hour)
Goal: Implement binary_to_decimal(s) that returns an integer.
Test cases:
binary_to_decimal("0") -> 0
binary_to_decimal("1") -> 1
binary_to_decimal("1010") -> 10
binary_to_decimal("11111111") -> 255
You understand: Summing powers of the base works.
Milestone 3: Hexadecimal Conversions (1-2 hours)
Goal: Add hex support with proper character mapping.
Test cases:
decimal_to_hex(0) -> "0"
decimal_to_hex(15) -> "F"
decimal_to_hex(255) -> "FF"
decimal_to_hex(256) -> "100"
hex_to_decimal("A") -> 10
hex_to_decimal("FF") -> 255
hex_to_decimal("100") -> 256
You understand: The hex character mapping (0-9, A-F).
Milestone 4: Input Validation (1 hour)
Goal: Reject invalid input with meaningful errors.
Test cases:
validate("123", binary) -> Error: '2' and '3' not valid binary
validate("GG", hex) -> Error: 'G' not valid hex digit
validate("", decimal) -> Error: empty input
validate("-5", decimal) -> Error: negative numbers not supported
You understand: Defensive programming and user experience.
Milestone 5: Command-Line Interface (1-2 hours)
Goal: Accept arguments from the command line.
Test cases:
$ python converter.py --from dec --to bin 255
11111111
$ python converter.py --from hex --to dec FF
255
$ python converter.py --help
Usage: converter.py [OPTIONS]
...
You understand: CLI design and user interaction.
Milestone 6: Advanced Features (Optional, 2+ hours)
Goal: Add verbose mode, batch processing, direct binary<->hex conversion.
You understand: The nibble relationship and software polish.
Hints in Layers
If you get stuck while implementing this project, consult these hints in order. Do not skip ahead - the struggle is where the learning happens.
Layer 1: General Direction
Use this if you’re completely stuck on where to start.
- Break the problem into two separate functions: “any base to decimal” and “decimal to any base”
- All conversions can go through decimal as an intermediate step
- Start with decimal<->binary only, then add hexadecimal once that works
- Test each function independently before connecting them
- Write the algorithm on paper first, then translate to code
Layer 2: Algorithmic Hints
Use this if your logic isn’t producing correct results.
For “other base to decimal”:
- Start from the rightmost digit (position 0)
- For each digit, multiply it by (base^position) and add to running total
- Example:
'1011'binary = (1x2^3) + (0x2^2) + (1x2^1) + (1x2^0) = 8 + 0 + 2 + 1 = 11
For “decimal to other base”:
- Use a loop that continues while the number is greater than 0
- In each iteration:
remainder = number % base, thennumber = number // base - Collect the remainders in a list
- Don’t forget to reverse the list at the end! (or prepend instead of append)
For special case zero:
- Handle
0as a special case - return"0"immediately - Otherwise your loop never executes (0 is not > 0)
Layer 3: Implementation Hints
Use this if you’re stuck on specific coding details.
For hexadecimal digit conversion:
def hex_char_to_value(char):
"""Convert a single hex character to its numeric value."""
if char.isdigit():
return int(char)
else:
return ord(char.upper()) - ord('A') + 10
def value_to_hex_char(value):
"""Convert a numeric value (0-15) to its hex character."""
if value < 10:
return str(value)
else:
return chr(ord('A') + value - 10)
For input validation:
def is_valid_for_base(input_str, base):
"""Check if all characters are valid for the given base."""
valid_chars = '0123456789ABCDEF'[:base]
return all(c.upper() in valid_chars for c in input_str)
For handling prefixes:
def strip_prefix(input_str):
"""Remove common prefixes like 0x, 0b, #."""
if input_str.startswith(('0x', '0X', '0b', '0B')):
return input_str[2:]
if input_str.startswith('#'):
return input_str[1:]
return input_str
Layer 4: Debugging Hints
Use this if your code runs but gives wrong answers.
- Print intermediate values to see where the logic breaks:
print(f"After step {i}: number={number}, remainder={remainder}") -
Test with simple cases first: 0, 1, 2, 10, 15, 16, 255, 256
- Common bugs to check:
- Off-by-one errors in loop conditions
- Forgetting to reverse the result
- Using
/instead of//for integer division - Character case issues (‘a’ vs ‘A’)
- Empty string after removing prefix
- Verify with known values:
255 decimal = FF hex = 11111111 binary 256 decimal = 100 hex = 100000000 binary 10 decimal = A hex = 1010 binary
Layer 5: Optimization Hints
Use this after your solution works and you want to improve it.
- For binary<->hex, use direct nibble conversion instead of going through decimal:
NIBBLE_TO_HEX = { '0000': '0', '0001': '1', '0010': '2', '0011': '3', '0100': '4', '0101': '5', '0110': '6', '0111': '7', '1000': '8', '1001': '9', '1010': 'A', '1011': 'B', '1100': 'C', '1101': 'D', '1110': 'E', '1111': 'F' } - Add padding for alignment:
- Pad binary to multiples of 4 for hex conversion
- Pad binary to multiples of 8 for byte boundaries
-
Add a verbose mode that shows the step-by-step conversion process
- Support different output formats:
- Raw:
FF - Prefixed:
0xFF - Padded:
00FF - Separated:
FF FF FF FF
- Raw:
Common Pitfalls & Debugging
Problem 1: “Converting 0 returns an empty string”
- Why: The repeated-division algorithm stops immediately and never appends digits.
- Fix: Special-case
0at the top of your conversion function and return"0". - Quick test:
0 (dec) → 0 (bin) → 0 (hex)
Problem 2: “My binary/hex output is backwards”
- Why: In repeated division, you generate least-significant digits first.
- Fix: Reverse the collected digits at the end (or build the output by prepending).
- Quick test:
10 (dec)should be1010 (bin)andA (hex).
Problem 3: “Hex digits A–F are wrong”
- Why: Off-by-10 errors when mapping characters (
Ashould mean 10). - Fix: Centralize mapping functions (
hex_char_to_value,value_to_hex_char) and test them directly. - Quick test:
15 (dec) → F (hex)and0xCAFE → 51966 (dec).
Problem 4: “Lowercase input breaks”
- Why: Validation compares against uppercase alphabet only.
- Fix: Normalize input to a canonical form (e.g.,
upper()) for validation and parsing. - Quick test:
0xff,ff,FFshould all work identically.
Problem 5: “Prefix stripping deletes too much / too little”
- Why:
0x,0b, and#prefixes are optional; naive stripping can produce"". - Fix: Strip prefixes carefully and validate non-empty remaining content.
- Quick test: Reject
0xwith a clear error, accept#FF5733in hex mode.
Problem 6: “Leading zeros disappear (but I wanted them)”
- Why: Numeric conversion discards formatting by design.
- Fix: Decide on formatting policy: raw vs padded output. Provide an explicit
--pador--width. - Quick test:
0x0Ashould display asAin raw mode and0Ain padded mode.
Testing Strategy
You learn faster when your converter can prove itself right.
- Unit tests (table-driven):
0, 1, 2, 7, 8, 15, 16, 31, 32, 255, 256, 4095, 4096- Known identities:
255 == 0xFF == 0b11111111
- Round-trip tests:
n → baseX → base10must equalnn → baseX → baseY → baseXmust preserve value (formatting may differ)
- Cross-check oracle (tests only):
- It’s fine to use
int(value, base)in tests to validate your own algorithms.
- It’s fine to use
- Input validation tests:
- Invalid characters, empty strings after prefix stripping, whitespace,
+/-handling policy
- Invalid characters, empty strings after prefix stripping, whitespace,
Definition of Done
--from/--to(or equivalent) supports at leastdec,bin,hex(bonus: base 2–36)- Conversion logic is implemented manually (no
bin(),hex(),int(x, base)in production code) - Accepts common prefixes (
0x,0b, optionally#) and handles upper/lowercase - Prints clear errors and non-zero exit codes for invalid input
- Handles
0correctly and has a documented policy for padding/leading zeros - Has automated tests (unit + round-trip) and they pass locally
- Includes
--helpoutput and at least 3 usage examples in the project notes/README
Books That Will Help
This table maps specific concepts in this project to exact chapters in recommended books:
| Topic | Book | Chapter/Section | Why This Helps |
|---|---|---|---|
| Positional Number Systems | “Code: The Hidden Language of Computer Hardware and Software” by Charles Petzold | Chapter 7: Counting, Chapter 8: Binary Arithmetic | Builds from first principles; shows why binary is fundamental |
| Base Conversion Algorithms | “Introduction to Algorithms” (CLRS) | Chapter 3: Growth of Functions | Mathematical rigor behind why these algorithms work |
| Algorithm Design | “Grokking Algorithms” by Aditya Bhargava | Chapter 1: Introduction | Visual, intuitive approach to algorithmic thinking |
| String Manipulation (Python) | “Automate the Boring Stuff with Python” by Al Sweigart | Chapter 6: Manipulating Strings | Practical string operations for parsing |
| Command-Line Tools | “Python Cookbook” by Beazley & Jones | Chapter 13: Utility Scripting | Real-world CLI patterns with argparse |
| Number Representation | “Computer Systems: A Programmer’s Perspective” (CS:APP) | Chapter 2: Representing and Manipulating Information | How computers actually store integers |
| JavaScript Basics | “Eloquent JavaScript” by Marijn Haverbeke | Chapter 4: Data Structures | If implementing in JS |
| Bitwise Operations | “Hacker’s Delight” by Henry S. Warren Jr. | Chapter 1: Basics | Advanced optimization techniques |
| Error Handling | “The Pragmatic Programmer” by Hunt & Thomas | Topic 23: Design by Contract | Philosophy of input validation |
| Testing | “Test-Driven Development with Python” by Percival | Part I: The Basics | How to write tests for your functions |
Recommended Reading Order
- Before coding: Petzold Chapters 7-8, Bhargava Chapter 1
- During implementation: Sweigart Chapter 6 (for string handling)
- After basic version works: CS:APP Chapter 2 (deeper understanding)
- For advanced features: Beazley Chapter 13, Warren’s “Hacker’s Delight”
Free Online Resources
- Khan Academy: “Binary and Hexadecimal Number Systems” (interactive exercises)
- Wikipedia: “Positional notation” (mathematical foundation)
- Python documentation:
argparsemodule (official reference) - realpython.com: Command-Line Interfaces tutorials
Self-Assessment Checklist
Before moving to the next project, verify you can:
Conceptual Understanding
- Explain why
255 = FF = 11111111without hesitation - Convert a 3-digit decimal to binary on paper in under 2 minutes
- Convert binary to hex using the nibble trick instantly
- Explain why hex is preferred over binary for displaying bytes
- Describe the division-remainder algorithm from memory
Implementation Skills
- Write
decimal_to_binary()from scratch without looking at references - Write
binary_to_decimal()from scratch without looking at references - Handle the hex character mapping (0-9, A-F) correctly
- Validate input and provide meaningful error messages
- Build a proper CLI interface with help text
Edge Cases
- Your code handles input
0correctly (returns"0", not"") - Your code handles single-digit inputs correctly
- Your code rejects invalid characters with clear error messages
- Your code handles uppercase and lowercase hex digits
- Your code handles optional prefixes (0x, 0b)
Interview Readiness
- Can answer “How would you convert decimal to binary?” clearly
- Can answer “Why do we use hexadecimal?” convincingly
- Can manually calculate
0xCAFEin decimal - Can explain the time complexity of your conversion algorithms
Final Milestone
You instinctively see numbers as abstract values with multiple representations. When you see 0xFF, you immediately think “255, all bits set, maximum byte value” without conscious effort.
What’s Next?
With base conversion mastered, you now understand the fundamental way computers represent information. In Project 2: Hexadecimal Color Visualizer, you’ll apply this knowledge to build an interactive web tool that shows how hex codes like #FF5733 directly correspond to RGB color values. You’ll see your binary/hex understanding come alive visually.
Quick Reference Card
Keep this handy while working:
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
BINARY/HEX QUICK REFERENCE
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
NIBBLE TABLE (Memorize This!)
─────────────────────────────
0=0000 4=0100 8=1000 C=1100
1=0001 5=0101 9=1001 D=1101
2=0010 6=0110 A=1010 E=1110
3=0011 7=0111 B=1011 F=1111
POWERS OF 2
───────────
2^0 = 1 2^4 = 16 2^8 = 256
2^1 = 2 2^5 = 32 2^9 = 512
2^2 = 4 2^6 = 64 2^10 = 1024
2^3 = 8 2^7 = 128 2^16 = 65536
POWERS OF 16
────────────
16^0 = 1 16^2 = 256 16^4 = 65536
16^1 = 16 16^3 = 4096 16^5 = 1048576
COMMON VALUES
─────────────
0xFF = 255 (max byte)
0x100 = 256 (1 more than max byte)
0xFFFF = 65535 (max 16-bit)
0xFFFFFFFF = 4,294,967,295 (max 32-bit)
ALGORITHMS
──────────
To Decimal: Sum of (digit × base^position)
To Other Base: Collect remainders of repeated division
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━

Remember: The goal isn’t just to build a working converter. It’s to internalize number representations so deeply that you think in multiple bases naturally. Take your time, do the paper exercises, and understand why each step works before coding it.