Project 2: Implement a Scheme/Lisp Interpreter
Project Overview
| Attribute | Value |
|---|---|
| Difficulty | Advanced |
| Time Estimate | 2-3 weeks |
| Main Language | Haskell |
| Alternatives | OCaml, Rust, Python |
| Prerequisites | Recursion, tree data structures, basic FP concepts |
| Key FP Concepts | Closures, lexical scoping, first-class functions, homoiconicity |
Learning Objectives
By completing this project, you will:
- Understand closures mechanically - See exactly how functions “capture” their environment
- Master lexical scoping - Understand why scope chains work the way they do
- Implement first-class functions - Make functions truly be values you can pass and return
- Grasp “code as data” - Experience homoiconicity and see why Lisp is special
- Implement recursion - See how recursive functions work at the interpreter level
- Understand evaluation - Programs are just data structures being transformed
The Core Question
“What happens when you call a function that ‘remembers’ variables from where it was defined? How do closures actually work?”
This is the most profound question in functional programming. A closure is a function bundled with its environment—the variables that were in scope when it was created. Understanding this mechanically (by building it) unlocks deep intuition about:
- Why lambdas can access outer variables
- How JavaScript callbacks work
- Why React hooks have “stale closure” bugs
- How currying and partial application work
Deep Theoretical Foundation
1. What Is Lisp?
Lisp (LISt Processing) is one of the oldest programming languages (1958), and every functional language descends from it. Its key insight: programs and data have the same structure.
In most languages, code and data are different:
# Python: code and data are separate
code = "def add(a, b): return a + b" # This is a string
data = [1, 2, 3] # This is data
In Lisp, code is data:
; Scheme: code IS data (both are lists)
(define code '(+ 1 2)) ; This is a list containing symbols
(eval code) ; → 3 (we can execute the list!)
This property is called homoiconicity (“same representation”).
2. S-Expressions: The Universal Syntax
Lisp uses S-expressions (symbolic expressions) for everything:
S-expression = atom | (S-expression*)
atom = number | symbol | string | boolean
Examples:
42 ; atom (number)
hello ; atom (symbol)
(+ 1 2) ; list of three elements: symbol +, number 1, number 2
(define x 10) ; list of three elements: symbol define, symbol x, number 10
((lambda (x) (* x x)) 5) ; nested lists (a function call!)
The first element of a list is usually an operator/function, the rest are arguments:
(operator arg1 arg2 ...)
3. Evaluation Rules
The Lisp evaluator follows these rules:
- Numbers, strings, booleans evaluate to themselves
- Symbols look up their value in the current environment
- Lists are function calls: evaluate the first element to get a function, evaluate the rest to get arguments, apply the function
; Rule 1: Self-evaluating
42 ; → 42
"hello" ; → "hello"
#t ; → #t (true)
; Rule 2: Symbol lookup
x ; → (whatever x is bound to in the environment)
; Rule 3: Function application
(+ 1 2) ; → 3
; 1. Evaluate + → <primitive procedure>
; 2. Evaluate 1 → 1
; 3. Evaluate 2 → 2
; 4. Apply + to (1, 2) → 3
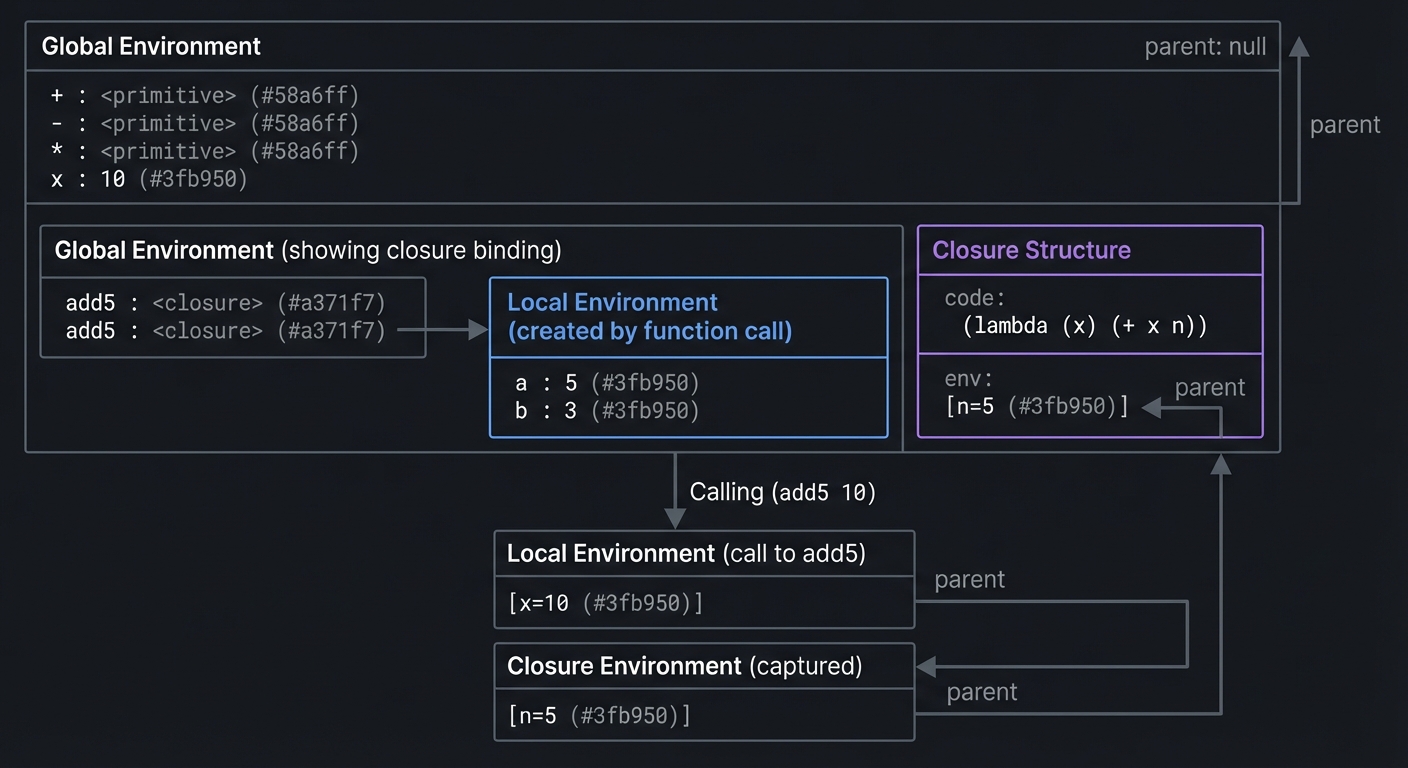
4. Environments and Scope
An environment is a mapping from names to values, plus a pointer to an enclosing environment:
Global Environment
├── + : <primitive>
├── - : <primitive>
├── * : <primitive>
└── x : 10
↑ (parent pointer)
Local Environment (created by function call)
├── a : 5
└── b : 3
When looking up a variable:
- Check the current environment
- If not found, check the parent environment
- Continue until found or reach global (error if not found)
This is lexical scoping: a variable’s binding is determined by where it appears in the source code, not where it’s called from.
5. Closures: The Heart of FP
A closure is a function plus the environment where it was defined:
(define (make-adder n)
(lambda (x) (+ x n))) ; This lambda "closes over" n
(define add5 (make-adder 5))
(add5 10) ; → 15
When (make-adder 5) executes:
- A new environment is created with
n = 5 - The
lambdais evaluated, creating a closure - The closure captures the environment where
n = 5 add5is bound to this closure
When (add5 10) executes:
- A new environment is created with
x = 10 - The parent of this environment is the closure’s captured environment (where
n = 5) (+ x n)is evaluated:xis 10,nis 5 → 15
Global Environment
└── add5 : <closure>
├── code: (lambda (x) (+ x n))
└── env: [n=5] → Global
When calling (add5 10):
[x=10] → [n=5] → Global

6. Special Forms
Not everything in Lisp follows the “evaluate all arguments” rule. Special forms have custom evaluation:
| Form | Behavior |
|---|---|
(define name value) |
Bind name to evaluated value; don’t evaluate name |
(lambda (params) body) |
Create closure; don’t evaluate params or body yet |
(if test then else) |
Evaluate test; then evaluate either then or else |
(quote expr) |
Return expr unevaluated |
(let ((x v) ...) body) |
Create local bindings |
(define x 10) ; define is special: x is not evaluated
(if (> x 5) ; if is special: only one branch is evaluated
"big"
"small") ; → "big"
(quote (+ 1 2)) ; quote is special: returns the list, doesn't evaluate
; → (+ 1 2) (not 3!)
7. Recursion Without Loops
Lisp has no for or while loops. All iteration is recursion:
(define (factorial n)
(if (<= n 1)
1
(* n (factorial (- n 1)))))
(factorial 5) ; → 120
Trace of (factorial 5):
(factorial 5)
(* 5 (factorial 4))
(* 5 (* 4 (factorial 3)))
(* 5 (* 4 (* 3 (factorial 2))))
(* 5 (* 4 (* 3 (* 2 (factorial 1)))))
(* 5 (* 4 (* 3 (* 2 1))))
(* 5 (* 4 (* 3 2)))
(* 5 (* 4 6))
(* 5 24)
120
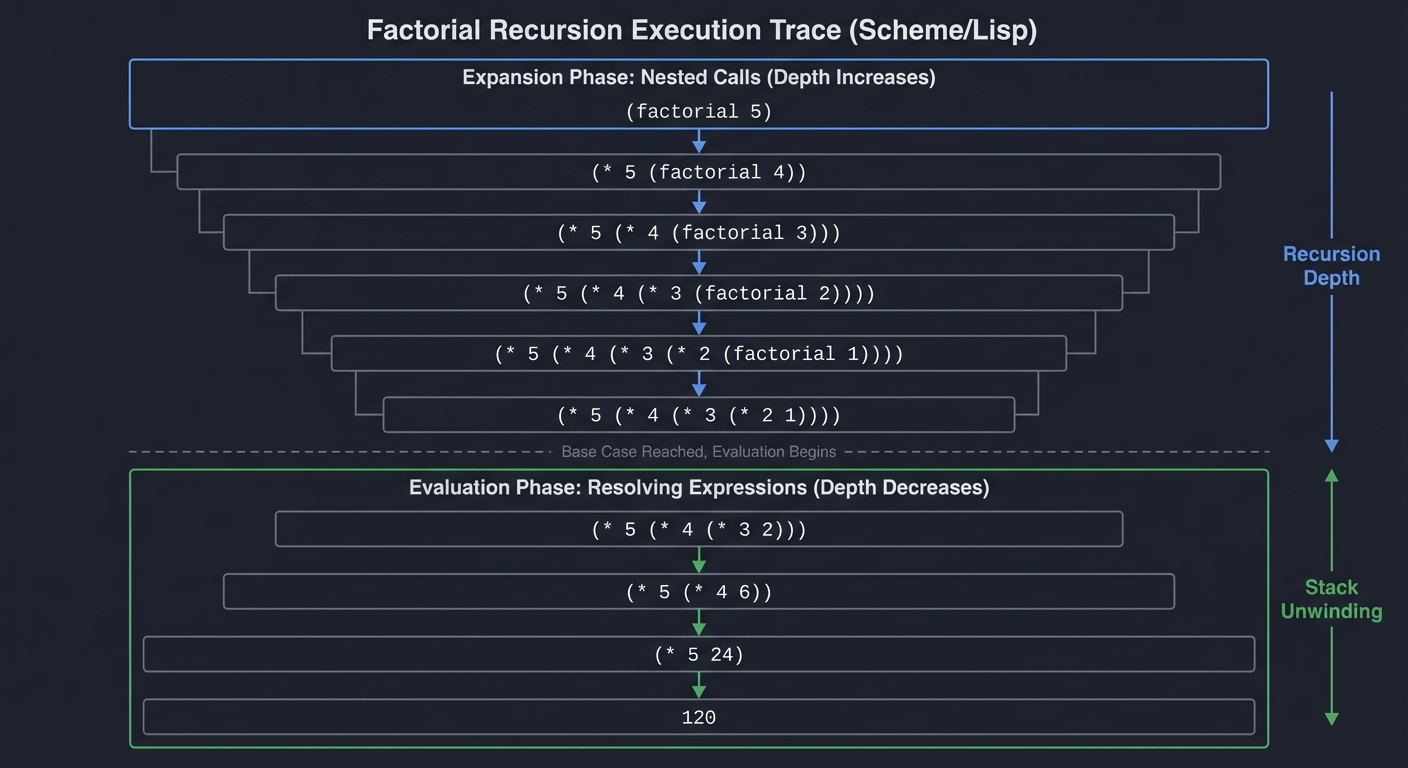
8. Tail-Call Optimization
Tail position: An expression is in tail position if it’s the last thing evaluated before returning.
; NOT tail-recursive: (* n ...) is the last thing, not the recursive call
(define (factorial n)
(if (<= n 1)
1
(* n (factorial (- n 1)))))
; Tail-recursive: (factorial-helper ...) is in tail position
(define (factorial n)
(define (helper n acc)
(if (<= n 1)
acc
(helper (- n 1) (* n acc)))) ; Last operation is the call itself
(helper n 1))
With tail-call optimization (TCO), tail-recursive calls don’t grow the stack. The interpreter can reuse the current stack frame. This makes recursion as efficient as iteration.
Project Specification
What You’re Building
A REPL (Read-Eval-Print Loop) for a subset of Scheme:
> (define x 10)
x
> x
10
> (+ x 5)
15
> (define (square n) (* n n))
square
> (square 7)
49
> (define (factorial n)
(if (<= n 1)
1
(* n (factorial (- n 1)))))
factorial
> (factorial 10)
3628800
> (map (lambda (x) (* x x)) '(1 2 3 4 5))
(1 4 9 16 25)
Language Features to Implement
Phase 1: Core
- Integers and arithmetic (
+,-,*,/) - Boolean values (
#t,#f) and comparisons (<,>,=,<=,>=) ifconditionaldefinefor variableslambdafor functions- Function application
Phase 2: Extended
- Symbols and
quote - Lists:
cons,car,cdr,list,null? letbindingsand,or,not
Phase 3: Higher-Order
map,filter,reduce- Variadic functions
- Tail-call optimization
Grammar
program = expression*
expression = atom | list
atom = number | boolean | string | symbol
list = "(" expression* ")"
number = [+-]?[0-9]+("."[0-9]+)?
boolean = "#t" | "#f"
string = "\"" [^"]* "\""
symbol = [a-zA-Z+\-*/<>=!?][a-zA-Z0-9+\-*/<>=!?_]*
Solution Architecture
Data Types
-- Lisp values
data LispVal
= Atom String -- Symbols like 'x', '+', 'define'
| List [LispVal] -- Lists like (+ 1 2)
| Number Double -- Numbers like 42, 3.14
| String String -- Strings like "hello"
| Bool Bool -- #t and #f
| PrimitiveFunc ([LispVal] -> Either LispError LispVal)
| Func { params :: [String]
, body :: LispVal
, closure :: Env -- The captured environment!
}
| Nil -- Empty list / null
-- Environment: a chain of frames
type Env = IORef [(String, IORef LispVal)]
-- Or for simplicity (without mutation):
data Env = Env
{ bindings :: Map String LispVal
, parent :: Maybe Env
}
-- Errors
data LispError
= NumArgs Integer [LispVal] -- Wrong number of arguments
| TypeMismatch String LispVal -- Wrong type
| UnboundVar String -- Undefined variable
| BadSpecialForm String LispVal -- Malformed special form
| NotFunction LispVal -- Tried to call non-function
| ParseError ParseError -- Syntax error
Core Functions
-- Parser: String → LispVal
parse :: String -> Either ParseError LispVal
-- Evaluator: LispVal + Env → Result
eval :: Env -> LispVal -> IO (Either LispError LispVal)
-- Environment operations
lookupVar :: Env -> String -> IO (Either LispError LispVal)
defineVar :: Env -> String -> LispVal -> IO ()
bindVars :: Env -> [(String, LispVal)] -> IO Env
-- Apply a function to arguments
apply :: LispVal -> [LispVal] -> IO (Either LispError LispVal)
Module Structure
src/
├── Main.hs # REPL entry point
├── Types.hs # LispVal, LispError, Env
├── Parser.hs # S-expression parser
├── Eval.hs # Evaluator
├── Env.hs # Environment operations
├── Primitives.hs # Built-in functions (+, -, cons, etc.)
└── Repl.hs # Read-Eval-Print loop
Implementation Guide
Phase 1: Parser (Days 1-3)
Goal: Parse S-expressions into LispVal.
Use Parsec (Haskell), nom (Rust), or write a simple recursive descent parser.
-- Parse an atom
parseAtom :: Parser LispVal
parseAtom = do
first <- letter <|> symbol
rest <- many (letter <|> digit <|> symbol)
let atom = first : rest
return $ case atom of
"#t" -> Bool True
"#f" -> Bool False
_ -> Atom atom
-- Parse a number
parseNumber :: Parser LispVal
parseNumber = Number . read <$> many1 digit
-- Parse a list
parseList :: Parser LispVal
parseList = List <$> sepBy parseExpr spaces
-- Parse any expression
parseExpr :: Parser LispVal
parseExpr = parseAtom
<|> parseNumber
<|> parseString
<|> do char '('
x <- parseList
char ')'
return x
Test cases:
42 → Number 42
x → Atom "x"
(+ 1 2) → List [Atom "+", Number 1, Number 2]
(define x 5) → List [Atom "define", Atom "x", Number 5]
Phase 2: Basic Evaluator (Days 4-6)
Goal: Evaluate atoms, numbers, and arithmetic.
eval :: Env -> LispVal -> IO (Either LispError LispVal)
eval env val = case val of
-- Self-evaluating
Number n -> return $ Right $ Number n
String s -> return $ Right $ String s
Bool b -> return $ Right $ Bool b
-- Variable lookup
Atom name -> lookupVar env name
-- Function application
List (func : args) -> do
evaledFunc <- eval env func
evaledArgs <- mapM (eval env) args
case (evaledFunc, sequence evaledArgs) of
(Right f, Right as) -> apply f as
(Left err, _) -> return $ Left err
(_, Left err) -> return $ Left err
-- Empty list
List [] -> return $ Right Nil
Primitive operations:
primitives :: [(String, [LispVal] -> Either LispError LispVal)]
primitives =
[ ("+", numericOp (+))
, ("-", numericOp (-))
, ("*", numericOp (*))
, ("/", numericOp (/))
, ("<", numCmp (<))
, (">", numCmp (>))
, ("=", numCmp (==))
]
numericOp :: (Double -> Double -> Double) -> [LispVal] -> Either LispError LispVal
numericOp op [Number a, Number b] = Right $ Number (op a b)
numericOp _ args = Left $ NumArgs 2 args
Phase 3: Special Forms (Days 7-9)
Goal: Implement if, define, lambda.
eval env val = case val of
-- ... previous cases ...
-- Special forms
List [Atom "if", test, consequent, alternate] -> do
result <- eval env test
case result of
Right (Bool False) -> eval env alternate
Right _ -> eval env consequent
Left err -> return $ Left err
List [Atom "define", Atom var, form] -> do
result <- eval env form
case result of
Right val -> do
defineVar env var val
return $ Right $ Atom var
Left err -> return $ Left err
List [Atom "lambda", List params, body] -> do
let paramNames = map extractAtom params
return $ Right $ Func paramNames body env -- Capture the environment!
The crucial closure creation:
-- When evaluating (lambda (x) body), we create:
Func { params = ["x"]
, body = body
, closure = env -- THIS is where the magic happens
}
Phase 4: Function Application (Days 10-12)
Goal: Apply user-defined functions with proper scoping.
apply :: LispVal -> [LispVal] -> IO (Either LispError LispVal)
apply (PrimitiveFunc func) args = return $ func args
apply (Func params body closure) args = do
if length params /= length args
then return $ Left $ NumArgs (toInteger $ length params) args
else do
-- Create new environment with parameter bindings
-- Parent is the CLOSURE environment, not the caller's!
env <- bindVars closure (zip params args)
eval env body
apply notFunc _ = return $ Left $ NotFunction notFunc
This is the key insight: When applying a function, the new environment’s parent is the closure’s captured environment, not the environment where the function is being called.
Phase 5: Lists and Quote (Days 13-15)
Goal: Implement list operations.
-- Quote: don't evaluate the argument
List [Atom "quote", val] -> return $ Right val
-- List primitives
("cons", cons)
("car", car)
("cdr", cdr)
("list", list)
("null?", isNull)
cons :: [LispVal] -> Either LispError LispVal
cons [x, List xs] = Right $ List (x : xs)
cons [x, Nil] = Right $ List [x]
cons [_, y] = Left $ TypeMismatch "list" y
cons args = Left $ NumArgs 2 args
car :: [LispVal] -> Either LispError LispVal
car [List (x:_)] = Right x
car [List []] = Left $ TypeMismatch "non-empty list" (List [])
car args = Left $ NumArgs 1 args
Phase 6: Higher-Order Functions (Days 16-18)
Goal: Implement map, filter, reduce.
-- map: apply function to each element
mapFunc :: Env -> [LispVal] -> IO (Either LispError LispVal)
mapFunc env [func, List xs] = do
results <- mapM (\x -> apply func [x]) xs
return $ List <$> sequence results
mapFunc _ args = return $ Left $ NumArgs 2 args
-- filter: keep elements where predicate is true
filterFunc :: Env -> [LispVal] -> IO (Either LispError LispVal)
filterFunc env [pred, List xs] = do
results <- filterM (\x -> do
result <- apply pred [x]
case result of
Right (Bool True) -> return True
_ -> return False) xs
return $ Right $ List results
Phase 7: Tail-Call Optimization (Days 19-21)
Goal: Don’t grow the stack for tail calls.
Instead of recursive eval calls, use a trampoline:
data Trampoline a
= Done a
| More (IO (Trampoline a))
evalTrampoline :: Env -> LispVal -> Trampoline (Either LispError LispVal)
evalTrampoline env val = case val of
-- For tail calls, return More instead of recursing
List [Atom "if", test, consequent, alternate] ->
case evalImmediate env test of
Right (Bool False) -> More $ return $ evalTrampoline env alternate
Right _ -> More $ return $ evalTrampoline env consequent
Left err -> Done $ Left err
-- For function application in tail position
-- ... similar pattern
runTrampoline :: Trampoline a -> IO a
runTrampoline (Done a) = return a
runTrampoline (More m) = m >>= runTrampoline
Testing Strategy
Parser Tests
testParser :: Test
testParser = TestList
[ "parse number" ~: parse "42" ~?= Right (Number 42)
, "parse atom" ~: parse "hello" ~?= Right (Atom "hello")
, "parse list" ~: parse "(+ 1 2)" ~?= Right (List [Atom "+", Number 1, Number 2])
, "parse nested" ~: parse "((lambda (x) x) 5)" ~?=
Right (List [List [Atom "lambda", List [Atom "x"], Atom "x"], Number 5])
]
Evaluator Tests
testEval :: Test
testEval = TestList
[ "arithmetic" ~: evalStr "(+ 1 2)" ~?= Right (Number 3)
, "nested" ~: evalStr "(* (+ 1 2) (- 5 2))" ~?= Right (Number 9)
, "if true" ~: evalStr "(if #t 1 2)" ~?= Right (Number 1)
, "if false" ~: evalStr "(if #f 1 2)" ~?= Right (Number 2)
, "define and use" ~: evalStr "(begin (define x 10) x)" ~?= Right (Number 10)
, "lambda" ~: evalStr "((lambda (x) (* x x)) 5)" ~?= Right (Number 25)
]
Closure Tests (The Important Ones!)
testClosures :: Test
testClosures = TestList
[ "closure captures variable" ~:
evalStr "(begin (define (make-adder n) (lambda (x) (+ x n))) ((make-adder 5) 10))"
~?= Right (Number 15)
, "closure shadows variable" ~:
evalStr "(begin (define n 100) (define (make-adder n) (lambda (x) (+ x n))) ((make-adder 5) 10))"
~?= Right (Number 15) -- Uses n=5 from closure, not n=100 from global
, "multiple closures" ~:
evalStr "(begin (define (make-adder n) (lambda (x) (+ x n))) (define add3 (make-adder 3)) (define add7 (make-adder 7)) (+ (add3 10) (add7 10)))"
~?= Right (Number 30) -- 13 + 17
]
Recursion Tests
testRecursion :: Test
testRecursion = TestList
[ "factorial" ~:
evalStr "(begin (define (fact n) (if (<= n 1) 1 (* n (fact (- n 1))))) (fact 5))"
~?= Right (Number 120)
, "fibonacci" ~:
evalStr "(begin (define (fib n) (if (< n 2) n (+ (fib (- n 1)) (fib (- n 2))))) (fib 10))"
~?= Right (Number 55)
, "tail-recursive factorial" ~:
evalStr "(begin (define (fact n) (define (helper n acc) (if (<= n 1) acc (helper (- n 1) (* n acc)))) (helper n 1)) (fact 1000))"
~?= Right (Number largeFactorial) -- Should not stack overflow
]
Common Pitfalls and Debugging
Pitfall 1: Using Dynamic Scoping Instead of Lexical
Symptom: Closures don’t work correctly
(define n 100)
(define (make-adder n) (lambda (x) (+ x n)))
(define add5 (make-adder 5))
(add5 10) ; Should be 15, but you get 110
Cause: When evaluating (+ x n), you’re looking up n in the caller’s environment (where n is 100) instead of the closure’s environment (where n is 5).
Solution: Make sure function application uses the closure’s environment as the parent:
-- WRONG: Use current environment
apply (Func params body _) args currentEnv = do
env <- bindVars currentEnv (zip params args) -- Wrong parent!
eval env body
-- RIGHT: Use closure's environment
apply (Func params body closure) args = do
env <- bindVars closure (zip params args) -- Correct parent!
eval env body
Pitfall 2: Not Handling Special Forms
Symptom: (define x 10) tries to look up x before binding it
Cause: You’re evaluating all arguments before recognizing special forms.
Solution: Check for special forms before evaluating arguments:
eval env val = case val of
List [Atom "define", Atom var, form] -> ... -- Special: don't eval 'var'
List [Atom "lambda", ...] -> ... -- Special: don't eval body
List (func : args) -> ... -- Normal: eval everything
Pitfall 3: Forgetting to Evaluate Function Position
Symptom: ((lambda (x) x) 5) doesn’t work
Cause: Not evaluating the first element of a list before applying.
Solution:
eval env (List (func : args)) = do
evaledFunc <- eval env func -- Evaluate the function position!
evaledArgs <- mapM (eval env) args
apply evaledFunc evaledArgs
Pitfall 4: Recursive Functions Don’t Work
Symptom: (define (fact n) ... (fact ...)) gives “unbound variable: fact”
Cause: The function is bound after evaluating the lambda, so the closure doesn’t see itself.
Solution: Use a recursive binding (Y combinator style) or define in two steps:
-- When evaluating (define (fact n) body):
-- 1. Create a placeholder binding
-- 2. Evaluate the lambda (captures env with placeholder)
-- 3. Update the placeholder to point to the actual function
defineFunction env name params body = do
ref <- newIORef Nil -- Placeholder
let env' = extendEnv env name ref
let func = Func params body env' -- Captures env with self-reference
writeIORef ref func
Extensions and Challenges
Challenge 1: Macros
Implement Lisp macros—code that generates code:
(define-macro (when test . body)
`(if ,test (begin ,@body) #f))
(when (> x 5)
(print "big")
(print "number"))
; Expands to:
; (if (> x 5) (begin (print "big") (print "number")) #f)
Challenge 2: Continuations
Implement call/cc (call with current continuation):
(define (search-list pred lst)
(call/cc
(lambda (return)
(for-each
(lambda (x)
(if (pred x)
(return x)))
lst)
#f)))
(search-list even? '(1 3 5 6 7 9)) ; → 6
Challenge 3: Garbage Collection
Implement mark-and-sweep or reference counting for your environment.
Challenge 4: Compile to Bytecode
Instead of tree-walking interpretation, compile to a bytecode VM for performance.
Real-World Connections
Lisp in Industry
- Emacs: Written in Emacs Lisp
- AutoCAD: Uses AutoLISP
- Grammarly: Core engine in Clojure
- Nubank: $10B bank built on Clojure
Modern Languages Influenced by Lisp
| Language | Lisp Influence |
|---|---|
| JavaScript | First-class functions, closures, eval |
| Ruby | Blocks, functional features, metaprogramming |
| Python | Lambda, list comprehensions, map/filter |
| Swift | Closures, trailing closure syntax |
| Clojure | Direct descendant, running on JVM |
Concepts Lisp Pioneered
- Garbage collection
- Tree data structures as the default
- Conditional expressions (
ifreturns a value) - Recursion as primary control flow
- First-class functions and closures
- Read-Eval-Print Loop (REPL)
- Meta-circular evaluation
Resources
Essential Reading
| Topic | Resource |
|---|---|
| Interpreter design | Structure and Interpretation of Computer Programs Ch. 3-4 |
| Closures and scope | Haskell Programming from First Principles Ch. 7 |
| The Little Schemer | Complete book - learn to think recursively |
| Recursion | Learn You a Haskell Ch. 5 |
Implementation References
- Write Yourself a Scheme in 48 Hours - Classic Haskell tutorial
- mal (Make a Lisp) - Implementations in 80+ languages
- (How to Write a (Lisp) Interpreter (in Python)) - Peter Norvig’s tutorial
Standards and Specifications
Self-Assessment Checklist
Before considering this project complete, verify:
Parser
- Parses numbers (integers and floats)
- Parses symbols/atoms
- Parses strings
- Parses booleans (
#t,#f) - Parses nested lists
- Handles whitespace and comments
Basic Evaluation
- Numbers evaluate to themselves
- Symbols look up values in environment
- Arithmetic works:
+,-,*,/ - Comparisons work:
<,>,=
Special Forms
ifevaluates correct branchdefinebinds variableslambdacreates closuresquotereturns unevaluated expressionletcreates local bindings
Functions and Closures
- User-defined functions can be called
- Closures capture their defining environment
- Nested closures work correctly
- Recursive functions work
Lists
conscreates pairscarreturns first elementcdrreturns rest of listlistcreates listsnull?tests for empty list
Higher-Order Functions
mapapplies function to listfilterselects elements- Lambda expressions work as arguments
Quality
- REPL reads multiline expressions
- Error messages are helpful
- Tests cover edge cases
Interview Questions
Prepare to discuss these after completing the project:
- “What is a closure?”
- Expected: A function bundled with its defining environment
- “What’s the difference between lexical and dynamic scoping?”
- Expected: Lexical uses definition site, dynamic uses call site
- “How do you implement recursion in an interpreter?”
- Expected: Recursive functions must see themselves in their environment
- “What is tail-call optimization and why does it matter?”
- Expected: Reusing stack frames for tail calls, enabling recursion without overflow
- “What makes Lisp homoiconic?”
- Expected: Code and data have the same structure (S-expressions)
- “How would you implement a macro system?”
- Expected: Macros are functions that run at parse time, transforming code before evaluation
- “Explain the evaluation rules for Lisp.”
- Expected: Self-evaluating atoms, symbol lookup, list = function application, special forms