Project 2: Bitwise Data Inspector

Build a CLI tool that reveals exactly how the machine stores integers and floating-point numbers, making bit-level representation tangible and predictable.

Quick Reference

Attribute	Value
Difficulty	Intermediate
Time Estimate	Weekend - 2 weeks
Language	C (Alternatives: Rust, Zig, C++)
Prerequisites	Basic C operators, binary/hex comfort, Project 1 recommended
Key Topics	Two’s complement, IEEE-754, endianness, type casting, overflow
CS:APP Chapters	2, 3

Learning Objectives
Deep Theoretical Foundation
Project Specification
Solution Architecture
Implementation Guide
Testing Strategy
Common Pitfalls & Debugging
Extensions & Challenges
Real-World Connections
Resources
Self-Assessment Checklist

1. Learning Objectives

By completing this project, you will:

Master two’s complement representation: Instantly convert between decimal, binary, and hex for signed/unsigned integers; predict when overflow and underflow occur
Decode IEEE-754 floating-point: Extract sign, exponent, and mantissa fields; explain why 0.1 + 0.2 != 0.3 and recognize NaN/Infinity patterns
Understand endianness: Predict byte ordering on any architecture and correctly interpret multi-byte values in memory dumps
Reason about type conversions: Predict what happens during signed/unsigned casts, truncation, and sign extension without running code
Recognize dangerous patterns: Identify code vulnerable to integer overflow, signed comparison bugs, and floating-point precision loss
Build intuition for bit manipulation: Perform shifts, masks, and bitwise operations mentally with confidence

2. Deep Theoretical Foundation

2.1 Why Binary Matters

At the hardware level, everything is binary. Your CPU, memory, and storage know nothing about “42” or “3.14”—they only see patterns of 0s and 1s. Understanding these patterns is essential because:

Overflow bugs cause security vulnerabilities and crashes
Precision loss corrupts financial calculations and scientific results
Comparison failures break sorting and searching algorithms
Memory corruption happens when you misunderstand data layout

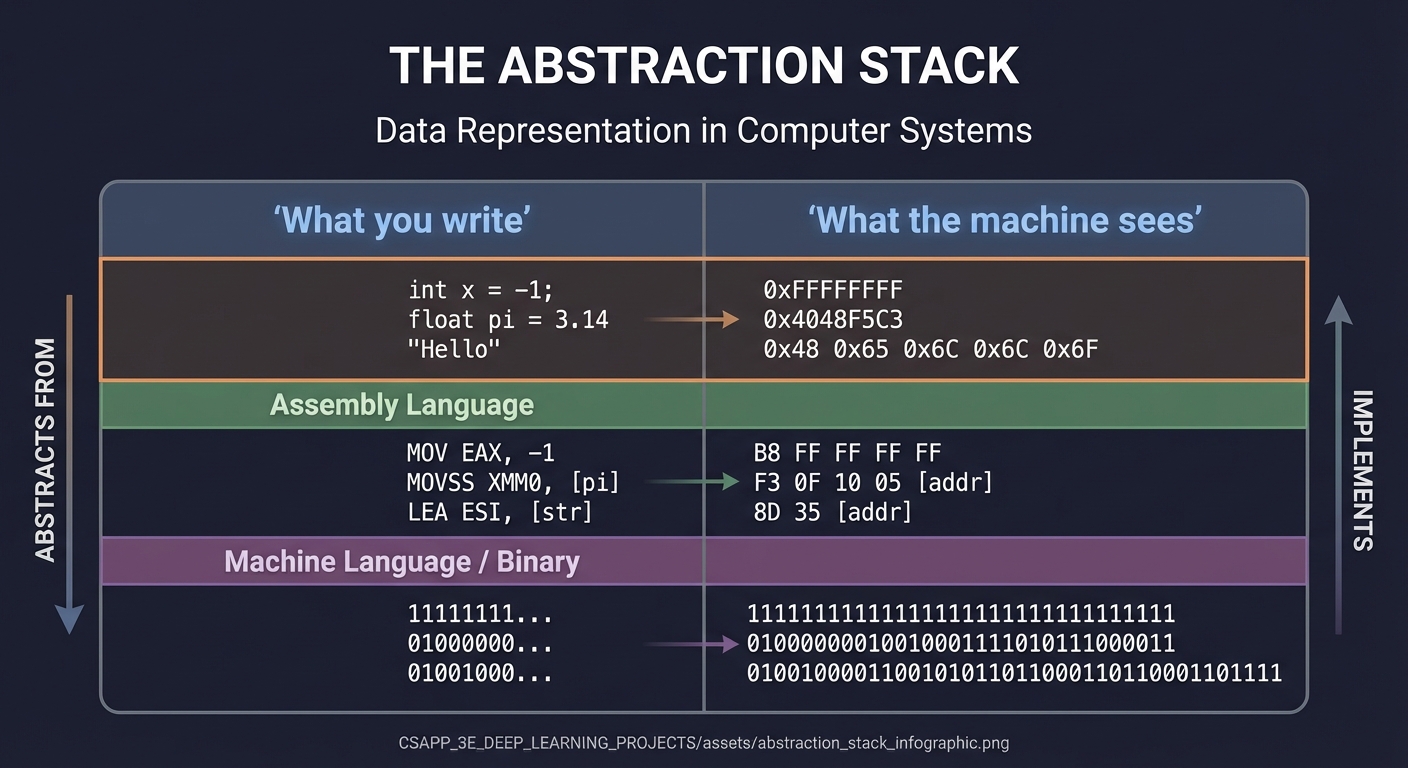
                    THE ABSTRACTION STACK

         What you write         What the machine sees
         ──────────────         ────────────────────
         int x = -1;      →     0xFFFFFFFF
         float pi = 3.14  →     0x4048F5C3
         "Hello"          →     0x48 0x65 0x6C 0x6C 0x6F

2.2 Unsigned Integers

Unsigned integers are the simplest representation: pure positional binary.

         UNSIGNED INTEGER: 8-bit example
         ═══════════════════════════════

         Binary: 1 0 1 1 0 1 1 0
                 │ │ │ │ │ │ │ │
                 │ │ │ │ │ │ │ └── 2^0 × 0 =   0
                 │ │ │ │ │ │ └──── 2^1 × 1 =   2
                 │ │ │ │ │ └────── 2^2 × 1 =   4
                 │ │ │ │ └──────── 2^3 × 0 =   0
                 │ │ │ └────────── 2^4 × 1 =  16
                 │ │ └──────────── 2^5 × 1 =  32
                 │ └────────────── 2^6 × 0 =   0
                 └──────────────── 2^7 × 1 = 128
                                           ─────
                                  Value:    182

         Formula: B2U(X) = Σ(i=0 to w-1) xᵢ × 2^i

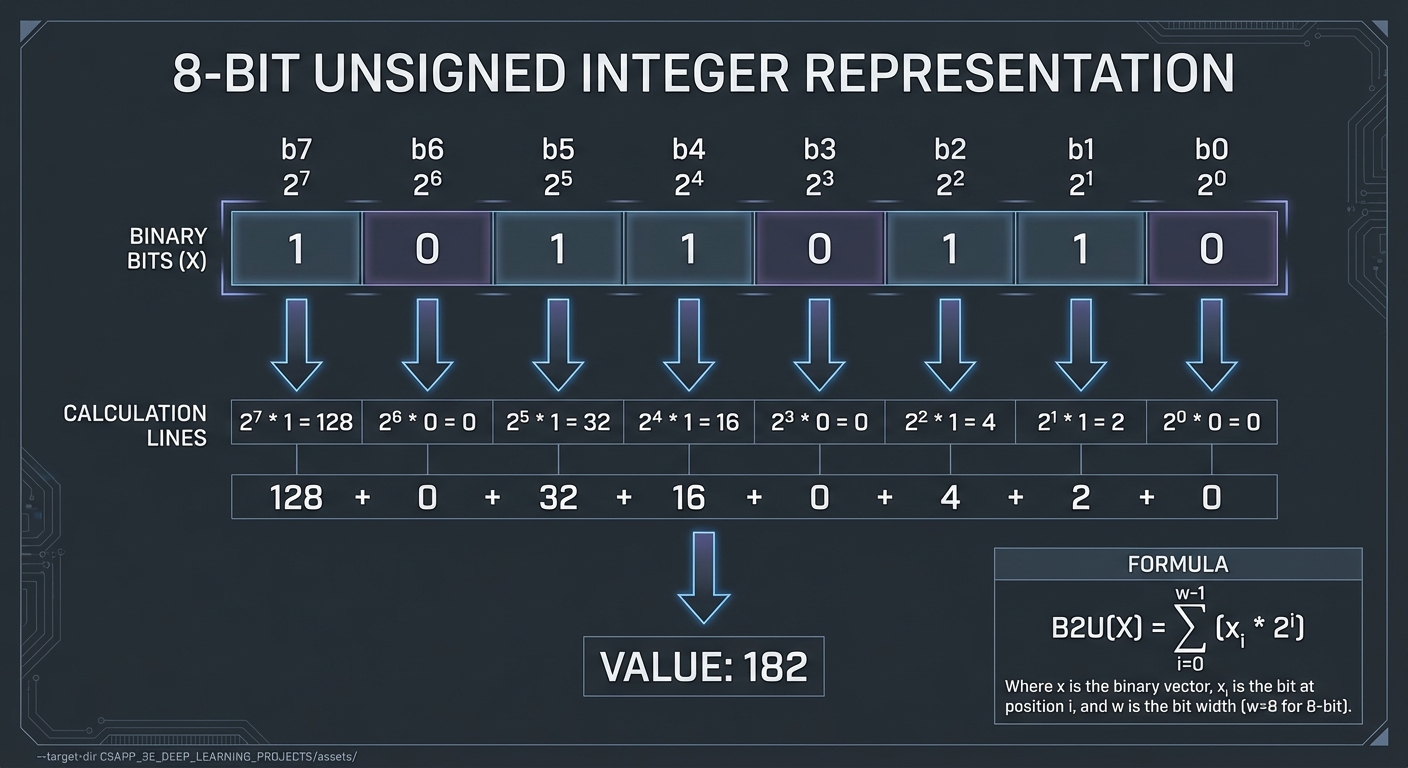
Range for w bits: 0 to 2^w - 1

Bits	Type (C)	Max
8	`unsigned char`	255
16	`unsigned short`	65,535
32	`unsigned int`	4,294,967,295
64	`unsigned long`	18,446,744,073,709,551,615

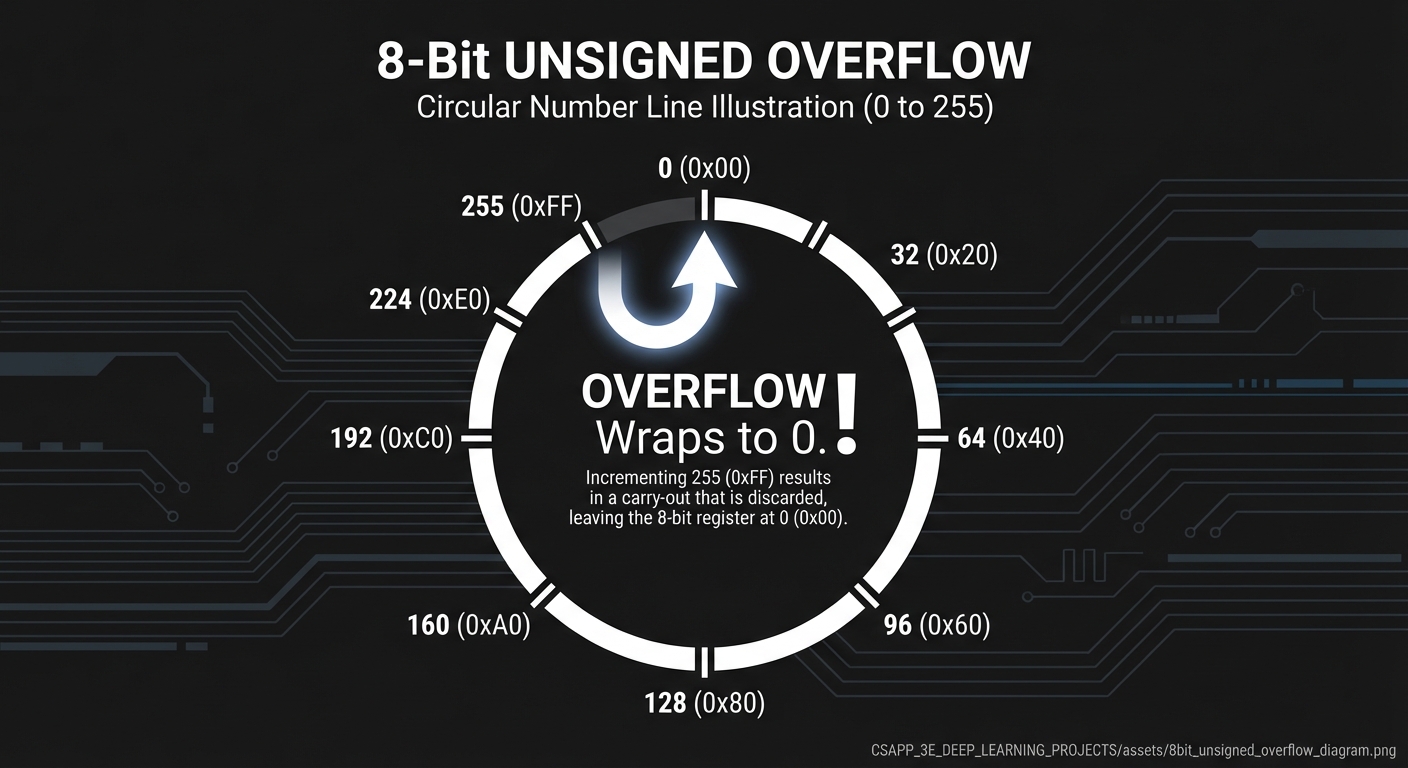
Overflow behavior: Wraps around modulo 2^w

         UNSIGNED OVERFLOW VISUALIZATION (8-bit)
         ═══════════════════════════════════════

         254 (0xFE)  →  255 (0xFF)  →  0 (0x00)  →  1 (0x01)
                            │
                            └── OVERFLOW! Wraps to 0

         The number line is actually a circle:

                     255 ──── 0
                    /          \
                  254            1
                  /              \
                ...              ...
                  \              /
                  129          126
                    \          /
                     128 ─── 127

2.3 Signed Integers: Two’s Complement

Two’s complement is the universal encoding for signed integers. The key insight: the most significant bit has negative weight.

         TWO'S COMPLEMENT: 8-bit example
         ════════════════════════════════

         Binary: 1 0 1 1 0 1 1 0
                 │ │ │ │ │ │ │ │
                 │ │ │ │ │ │ │ └── 2^0 × 0 =    0
                 │ │ │ │ │ │ └──── 2^1 × 1 =    2
                 │ │ │ │ │ └────── 2^2 × 1 =    4
                 │ │ │ │ └──────── 2^3 × 0 =    0
                 │ │ │ └────────── 2^4 × 1 =   16
                 │ │ └──────────── 2^5 × 1 =   32
                 │ └────────────── 2^6 × 0 =    0
                 └──────────────── 2^7 × 1 = -128  ← NEGATIVE weight!
                                            ─────
                                  Value:    -74

         Formula: B2T(X) = -x_(w-1) × 2^(w-1) + Σ(i=0 to w-2) xᵢ × 2^i

Why two’s complement?

Single representation of zero: Unlike one’s complement or sign-magnitude
Hardware simplicity: Addition works the same for signed and unsigned
Easy negation: Flip bits and add 1

         NEGATION IN TWO'S COMPLEMENT
         ═════════════════════════════

         To negate a number: flip all bits, then add 1

         Example: negate 5 (8-bit)

           5 = 0000 0101
         ~5  = 1111 1010      (flip all bits)
         +1  = 1111 1011      (add 1)
          -5 = 1111 1011      (result: -5)

         Verify: -128 + 64 + 32 + 16 + 8 + 2 + 1 = -5 ✓

Range for w bits: -2^(w-1) to 2^(w-1) - 1

Bits	Type (C)	Min	Max
8	`signed char`	-128	127
16	`short`	-32,768	32,767
32	`int`	-2,147,483,648	2,147,483,647
64	`long`	-9,223,372,036,854,775,808	9,223,372,036,854,775,807

Critical asymmetry:

TMin

TMax

+ 1

         THE TWO'S COMPLEMENT NUMBER LINE (4-bit example)
         ═══════════════════════════════════════════════

         Binary    Unsigned    Signed
         ──────    ────────    ──────
         0000         0           0
         0001         1           1
         0010         2           2
         0011         3           3
         0100         4           4
         0101         5           5
         0110         6           6
         0111         7           7    ← Maximum positive
         ────────────────────────────
         1000         8          -8    ← TMin (no positive equivalent!)
         1001         9          -7
         1010        10          -6
         1011        11          -5
         1100        12          -4
         1101        13          -3
         1110        14          -2
         1111        15          -1

Signed overflow is UNDEFINED BEHAVIOR in C!

int x = INT_MAX;
x = x + 1;  // UNDEFINED! Compiler can do anything

2.4 Sign Extension and Truncation

When converting between different bit widths, you must handle the bits correctly.

Sign Extension (smaller to larger): Copy the sign bit into new positions

         SIGN EXTENSION: 8-bit to 16-bit
         ═════════════════════════════

         Positive number (5):
         0000 0101            →    0000 0000 0000 0101
         │                         ││││ ││││
         └─ sign bit is 0          └┴┴┴─┴┴┴┴── copy 0s into high bits

         Negative number (-5):
         1111 1011            →    1111 1111 1111 1011
         │                         ││││ ││││
         └─ sign bit is 1          └┴┴┴─┴┴┴┴── copy 1s into high bits

         This preserves the numeric value!

Zero Extension (unsigned): Always fill with zeros

         ZERO EXTENSION: 8-bit unsigned to 16-bit
         ═════════════════════════════════════════

         182 unsigned:
         1011 0110            →    0000 0000 1011 0110
                                   ││││ ││││
                                   └┴┴┴─┴┴┴┴── always fill with 0s

Truncation (larger to smaller): Keep only low-order bits

         TRUNCATION: 32-bit to 8-bit
         ═══════════════════════════

         0x12345678  →  0x78 (keep low byte only)

         Value changes! 305,419,896 → 120

         Effect: result = original mod 2^k
         where k = number of bits retained

2.5 Signed vs Unsigned Comparisons

When C compares signed and unsigned, it converts signed to unsigned first. This causes subtle bugs:

         DANGEROUS COMPARISON
         ═════════════════════

         int x = -1;
         unsigned int y = 0;

         if (x < y)     // What happens?
             printf("expected");
         else
             printf("SURPRISE!");

         Answer: SURPRISE!

         Why? x is converted to unsigned first:
              -1 as signed   = 0xFFFFFFFF
              Same bits as unsigned = 4,294,967,295

              4,294,967,295 > 0, so condition is FALSE

Conversion rules in C:

Expression Type	If one operand is	Other operand becomes
Comparison	`unsigned`	converted to `unsigned`
Arithmetic	`unsigned`	converted to `unsigned`
Assignment	target type	converted to target type

         COMPARISON CONVERSION TABLE
         ═══════════════════════════

         Type1       Type2        Comparison Type
         ─────       ─────        ───────────────
         int         int          signed
         unsigned    unsigned     unsigned
         int         unsigned     UNSIGNED ← danger!
         long        unsigned     depends on sizes

2.6 IEEE-754 Floating-Point Representation

Floating-point numbers use scientific notation in binary.

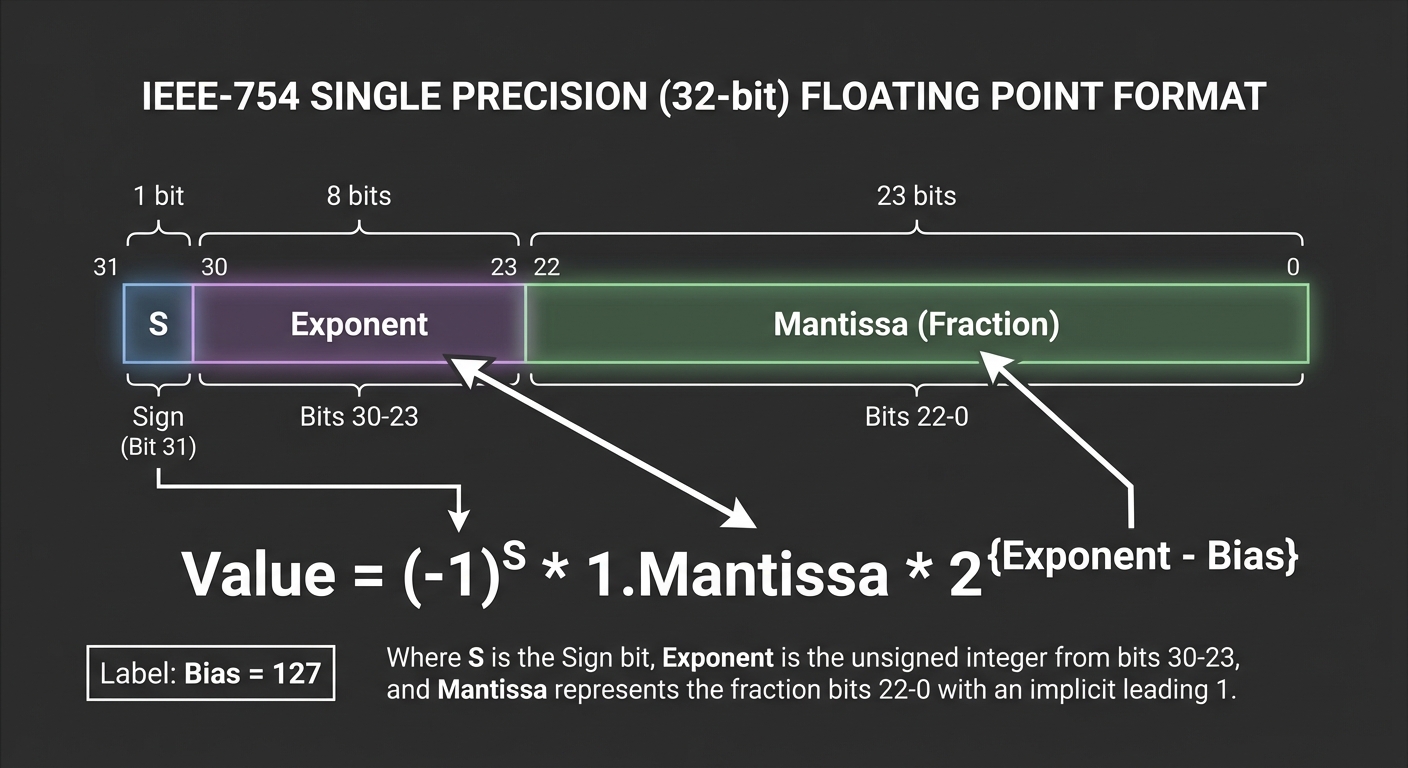
         IEEE-754 SINGLE PRECISION (32-bit)
         ═══════════════════════════════════

         ┌─────┬────────────────┬─────────────────────────────────────────────┐
         │  S  │   Exponent     │               Mantissa (Fraction)           │
         │ 1b  │    8 bits      │                   23 bits                   │
         └─────┴────────────────┴─────────────────────────────────────────────┘
         bit 31   bits 30-23                    bits 22-0

         Value = (-1)^S × 1.Mantissa × 2^(Exponent - Bias)

         Bias = 127 for single precision
         Bias = 1023 for double precision

Example: Encoding 13.625

         ENCODING 13.625 AS IEEE-754 SINGLE
         ═══════════════════════════════════

         Step 1: Convert to binary
                 13 = 1101 (binary)
                 0.625 = 0.101 (binary: 1/2 + 1/8)
                 13.625 = 1101.101

         Step 2: Normalize (scientific notation)
                 1101.101 = 1.101101 × 2^3
                            │       │
                            │       └── exponent = 3
                            └── mantissa (after the 1.)

         Step 3: Encode fields
                 Sign: 0 (positive)
                 Exponent: 3 + 127 = 130 = 1000 0010
                 Mantissa: 101 1010 0000 0000 0000 0000
                           (drop the implicit leading 1)

         Result: 0 10000010 10110100000000000000000
                 = 0x41590000

IEEE-754 Double Precision (64-bit)

         ┌─────┬──────────────────────┬──────────────────────────────────────────────────────────────────────┐
         │  S  │      Exponent        │                          Mantissa (Fraction)                        │
         │ 1b  │      11 bits         │                              52 bits                                │
         └─────┴──────────────────────┴──────────────────────────────────────────────────────────────────────┘
         bit 63    bits 62-52                                bits 51-0

2.7 Special Floating-Point Values

IEEE-754 reserves certain bit patterns for special values:

         SPECIAL VALUES IN IEEE-754
         ═══════════════════════════

         ┌────────────────────┬─────────────┬─────────────┬──────────────────┐
         │   Value            │  Exponent   │  Mantissa   │   Meaning        │
         ├────────────────────┼─────────────┼─────────────┼──────────────────┤
         │   +0.0             │  0000...0   │  0000...0   │  Positive zero   │
         │   -0.0             │  0000...0   │  0000...0   │  Negative zero   │
         │   Denormalized     │  0000...0   │  nonzero    │  Very small nums │
         │   Normalized       │  0<exp<max  │  any        │  Normal numbers  │
         │   +Infinity        │  1111...1   │  0000...0   │  Positive inf    │
         │   -Infinity        │  1111...1   │  0000...0   │  Negative inf    │
         │   NaN              │  1111...1   │  nonzero    │  Not a Number    │
         └────────────────────┴─────────────┴─────────────┴──────────────────┘

Denormalized (Subnormal) Numbers

When the exponent is all zeros, the implicit leading bit becomes 0 instead of 1. This allows representing numbers very close to zero:

         DENORMALIZED NUMBERS
         ═════════════════════

         Normal:      Value = 1.mantissa × 2^(exp - bias)
         Denormal:    Value = 0.mantissa × 2^(1 - bias)

         For single precision:
         Smallest normal:     1.0 × 2^-126  ≈ 1.18 × 10^-38
         Smallest denormal:   2^-23 × 2^-126 = 2^-149 ≈ 1.4 × 10^-45

         Denormals provide "gradual underflow" to zero

NaN Behavior

         NaN RULES
         ═════════

         NaN sources:
         - 0.0 / 0.0
         - infinity - infinity
         - infinity × 0
         - sqrt(-1)

         NaN properties:
         - NaN != NaN  (NaN is not equal to itself!)
         - NaN op anything = NaN (propagates)
         - x != x is TRUE only if x is NaN

2.8 Floating-Point Precision and Rounding

Floating-point cannot represent all real numbers exactly. Understanding this prevents bugs:

         WHY 0.1 + 0.2 != 0.3
         ═════════════════════

         0.1 in binary = 0.0001100110011001100110011...  (repeating!)

         This is like 1/3 in decimal: 0.333333...
         We can't store infinite digits, so we round.

         0.1 ≈ 0.10000000149... (single precision)
         0.2 ≈ 0.20000000298... (single precision)
         0.1 + 0.2 ≈ 0.30000000447...

         But 0.3 ≈ 0.30000001192...

         They're stored as different bit patterns!

Representable Numbers

         FLOATING-POINT NUMBER LINE (simplified)
         ═══════════════════════════════════════

         ─∞────┼────┼───┼──┼─┼┼┼┼┼┼┼┼┼┼┼┼┼┼─┼──┼───┼────┼────+∞
               │    │   │  │     0     │  │   │    │
               │    │   │  │           │  │   │    │
               │    │   │  │ very dense│  │   │    │
               │    │   │  │           │  │   │    │
               │    │   │  └───────────┘  │   │    │
               │    │   │   gaps grow →   │   │    │
               │    │   │                 │   │    │
               │    │   └── powers of 2 ──┘   │    │
               │    │       are EXACT         │    │
               │    │                         │    │

         Key insight: Precision is RELATIVE, not absolute.
         Large numbers have large gaps between representable values.

Rounding Modes

IEEE-754 defines rounding modes for when exact representation is impossible:

Mode	Description	Example (to integer)
Round to nearest even	Default; ties go to even	2.5 → 2, 3.5 → 4
Round toward +∞	Always round up	2.1 → 3, -2.9 → -2
Round toward -∞	Always round down	2.9 → 2, -2.1 → -3
Round toward 0	Truncate	2.9 → 2, -2.9 → -2

2.9 Endianness

Endianness determines byte ordering in multi-byte values.

         ENDIANNESS: Storing 0x12345678 in memory
         ═════════════════════════════════════════

         Address:    100   101   102   103
                     ─── ─ ─── ─ ─── ─ ───

         Big-Endian:  12    34    56    78     (most significant first)
         (Network)    MSB ────────────→ LSB

         Little-Endian: 78    56    34    12   (least significant first)
         (x86, ARM)     LSB ────────────→ MSB


         Memory dump showing 0x12345678:

         Big-Endian:    0x64: 12 34 56 78
                              │  │  │  └── address 103
                              │  │  └───── address 102
                              │  └──────── address 101
                              └─────────── address 100

         Little-Endian: 0x64: 78 56 34 12
                              │  │  │  └── address 103
                              │  │  └───── address 102
                              │  └──────── address 101
                              └─────────── address 100

Why It Matters

         ENDIANNESS BUGS
         ═══════════════

         Network protocol sends big-endian, your machine is little-endian:

         Sent: 0x01 0x00     (value 256 in big-endian)
         Received: interpreted as 0x0001 (value 1 in little-endian)

         This is why we have ntohl(), htonl(), etc.:
         - htons/htonl: host to network (convert to big-endian)
         - ntohs/ntohl: network to host (convert from big-endian)

Detecting Endianness

int is_little_endian(void) {
    unsigned int x = 1;
    return *((unsigned char *)&x) == 1;
}

2.10 Data Alignment and Padding

Processors access memory most efficiently at aligned addresses:

         ALIGNMENT REQUIREMENTS
         ══════════════════════

         Type          Typical Alignment    Size
         ────          ─────────────────    ────
         char          1 byte               1 byte
         short         2 bytes              2 bytes
         int           4 bytes              4 bytes
         long          8 bytes              8 bytes
         float         4 bytes              4 bytes
         double        8 bytes              8 bytes
         pointer       8 bytes (64-bit)     8 bytes

         "Aligned" means: address % alignment == 0

Struct Padding

         STRUCT PADDING EXAMPLE
         ══════════════════════

         struct bad_layout {    // 24 bytes due to padding!
             char a;            // offset 0, size 1
             // 7 bytes padding
             double b;          // offset 8, size 8 (must be 8-aligned)
             char c;            // offset 16, size 1
             // 3 bytes padding
             int d;             // offset 20, size 4 (must be 4-aligned)
         };

         Memory layout:
         ┌───┬───────────────┬───────────────────────────────┬───┬───────┬───────────────┐
         │ a │   padding     │              b                │ c │  pad  │       d       │
         ├───┼───┬───┬───┬───┼───┬───┬───┬───┬───┬───┬───┬───┼───┼───┬───┼───┬───┬───┬───┤
         │ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │ 8 │ 9 │10 │11 │12 │13 │14 │15 │16 │17 │18 │19 │
         └───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┴───┘

         struct good_layout {   // 16 bytes with smart ordering!
             double b;          // offset 0, size 8
             int d;             // offset 8, size 4
             char a;            // offset 12, size 1
             char c;            // offset 13, size 1
             // 2 bytes padding for struct alignment
         };

         Rule: Order struct members from largest to smallest!

3. Project Specification

3.1 What You Will Build

A command-line data inspector that takes numeric values and displays:

The exact byte-level representation
Interpretation under different type assumptions
Endianness information
Warnings about potential issues (overflow, precision loss, special values)

3.2 Functional Requirements

Input Modes:

Decimal integers: inspect 42, inspect -127
Hexadecimal: inspect 0xDEADBEEF
Binary: inspect 0b11010110
Floating-point: inspect 3.14159, inspect -0.0
Raw bytes: inspect --bytes "78 56 34 12"

Output Requirements:

Show all bytes in hex
Show binary representation
Show interpretation as:
- Unsigned integer (various sizes)
- Signed integer (various sizes)
- IEEE-754 float/double (with field breakdown)
Show endianness of current system
Explain any special values (NaN, Inf, TMin)

3.3 Example Usage and Output

$ ./bitwise-inspector 42

═══════════════════════════════════════════════════════════════════════════════
                         BITWISE DATA INSPECTOR
                              Input: 42
═══════════════════════════════════════════════════════════════════════════════

BYTE REPRESENTATION (on little-endian system)
─────────────────────────────────────────────
  Memory order:    2A 00 00 00 00 00 00 00
  Logical order:   00 00 00 00 00 00 00 2A

BINARY VIEW (64-bit)
─────────────────────────────────────────────
  0000 0000 0000 0000 0000 0000 0000 0000
  0000 0000 0000 0000 0000 0000 0010 1010
                                    └┴┴┴──── 2 + 8 + 32 = 42

INTEGER INTERPRETATIONS
─────────────────────────────────────────────
  Type             Hex            Decimal
  ────             ───            ───────
  uint8_t          0x2A           42
  int8_t           0x2A           42
  uint16_t         0x002A         42
  int16_t          0x002A         42
  uint32_t         0x0000002A     42
  int32_t          0x0000002A     42
  uint64_t         0x000000000000002A     42
  int64_t          0x000000000000002A     42

FLOATING-POINT INTERPRETATION
─────────────────────────────────────────────
  As float (32-bit):  5.885e-44  (denormalized!)
    │ Sign:     0 (positive)
    │ Exponent: 00000000 (0) → denormalized
    │ Mantissa: 00000000000000000101010
    └── Formula: 0.mantissa × 2^(-126) = 5.88545e-44

  As double (64-bit): 2.075e-322 (denormalized!)

SYSTEM INFO
─────────────────────────────────────────────
  Endianness:   Little-endian (x86-64)
  sizeof(int):  4 bytes
  sizeof(long): 8 bytes

═══════════════════════════════════════════════════════════════════════════════

$ ./bitwise-inspector -1

═══════════════════════════════════════════════════════════════════════════════
                         BITWISE DATA INSPECTOR
                              Input: -1
═══════════════════════════════════════════════════════════════════════════════

BYTE REPRESENTATION (on little-endian system)
─────────────────────────────────────────────
  Memory order:    FF FF FF FF FF FF FF FF
  Logical order:   FF FF FF FF FF FF FF FF

BINARY VIEW (64-bit)
─────────────────────────────────────────────
  1111 1111 1111 1111 1111 1111 1111 1111
  1111 1111 1111 1111 1111 1111 1111 1111
  │
  └── Sign bit = 1 (negative in signed interpretation)

INTEGER INTERPRETATIONS
─────────────────────────────────────────────
  Type             Hex            Decimal
  ────             ───            ───────
  uint8_t          0xFF           255
  int8_t           0xFF           -1
  uint16_t         0xFFFF         65535
  int16_t          0xFFFF         -1
  uint32_t         0xFFFFFFFF     4294967295
  int32_t          0xFFFFFFFF     -1
  uint64_t         0xFFFFFFFFFFFFFFFF     18446744073709551615
  int64_t          0xFFFFFFFFFFFFFFFF     -1

  ⚠ WARNING: Same bits, vastly different unsigned/signed values!
    Comparing as signed vs unsigned can cause bugs.

FLOATING-POINT INTERPRETATION
─────────────────────────────────────────────
  As float (32-bit):  NaN (quiet)
    │ Sign:     1 (negative)
    │ Exponent: 11111111 (255) → special value
    │ Mantissa: 11111111111111111111111 (non-zero) → NaN
    └── NaN: Not a Number (invalid operation result)

  As double (64-bit): NaN (quiet)

═══════════════════════════════════════════════════════════════════════════════

$ ./bitwise-inspector 0.1

═══════════════════════════════════════════════════════════════════════════════
                         BITWISE DATA INSPECTOR
                              Input: 0.1 (floating-point)
═══════════════════════════════════════════════════════════════════════════════

AS DOUBLE (64-bit IEEE-754)
─────────────────────────────────────────────
  Hex:      0x3FB999999999999A

  Binary breakdown:
  ┌───┬─────────────────────┬──────────────────────────────────────────────────────────────┐
  │ S │      Exponent       │                         Mantissa                              │
  │ 0 │ 0 1 1 1 1 1 1 1 0 1 1│ 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 0│
  └───┴─────────────────────┴──────────────────────────────────────────────────────────────┘
    │            │                                     │
    │            │                                     └── Repeating pattern!
    │            └── 1019 (biased) → 1019 - 1023 = -4
    └── Positive

  Stored value: +1.1001100110011001100110011001100110011001100110011010 × 2^(-4)
  Exact decimal: 0.1000000000000000055511151231257827021181583404541015625

  ⚠ PRECISION WARNING:
    Input 0.1 cannot be exactly represented in binary floating-point!
    Error: +5.55e-18 (about 1 part in 10^17)

AS FLOAT (32-bit IEEE-754)
─────────────────────────────────────────────
  Hex:      0x3DCCCCCD

  Stored value: +1.10011001100110011001101 × 2^(-4)
  Exact decimal: 0.10000000149011611938476562500000

  ⚠ PRECISION WARNING:
    Float has less precision than double.
    Converting 0.1 to float loses ~7 decimal digits of precision.

═══════════════════════════════════════════════════════════════════════════════

$ ./bitwise-inspector --bytes "00 00 80 7F"

═══════════════════════════════════════════════════════════════════════════════
                         BITWISE DATA INSPECTOR
                              Input: raw bytes 00 00 80 7F
═══════════════════════════════════════════════════════════════════════════════

RAW BYTES
─────────────────────────────────────────────
  As entered:     00 00 80 7F
  Reversed:       7F 80 00 00

INTEGER INTERPRETATIONS (assuming little-endian input)
─────────────────────────────────────────────
  uint32_t (LE):  0x7F800000     2139095040
  int32_t (LE):   0x7F800000     2139095040
  uint32_t (BE):  0x0000807F     32895
  int32_t (BE):   0x0000807F     32895

FLOATING-POINT INTERPRETATION
─────────────────────────────────────────────
  As float (little-endian): +Infinity
    │ Sign:     0 (positive)
    │ Exponent: 11111111 (255) → special value
    │ Mantissa: 00000000000000000000000 (zero) → Infinity
    └── +Infinity: Result of overflow or 1/0

  ★ SPECIAL VALUE: This is IEEE-754 positive infinity!

═══════════════════════════════════════════════════════════════════════════════

4. Solution Architecture

4.1 High-Level Design

         ┌─────────────────────────────────────────────────────────────────────┐
         │                        BITWISE INSPECTOR                            │
         ├─────────────────────────────────────────────────────────────────────┤
         │                                                                     │
         │   ┌───────────────┐                                                 │
         │   │  Input Parser │◀── decimal, hex, binary, float, raw bytes      │
         │   └───────┬───────┘                                                 │
         │           │                                                         │
         │           ▼                                                         │
         │   ┌───────────────┐                                                 │
         │   │  Raw Bytes    │  Canonical internal representation              │
         │   │  (uint8_t[])  │  (always 8 bytes for simplicity)                │
         │   └───────┬───────┘                                                 │
         │           │                                                         │
         │     ┌─────┴─────┬─────────────────┬───────────────────┐            │
         │     ▼           ▼                 ▼                   ▼            │
         │ ┌────────┐ ┌──────────┐    ┌────────────┐    ┌─────────────┐       │
         │ │Integer │ │ Integer  │    │   Float    │    │   Special   │       │
         │ │Unsigned│ │ Signed   │    │   Parser   │    │   Values    │       │
         │ └────┬───┘ └────┬─────┘    └─────┬──────┘    └──────┬──────┘       │
         │      │          │                │                  │              │
         │      └──────────┴────────────────┴──────────────────┘              │
         │                              │                                      │
         │                              ▼                                      │
         │                     ┌─────────────────┐                            │
         │                     │ Report Generator│                            │
         │                     └────────┬────────┘                            │
         │                              │                                      │
         │                              ▼                                      │
         │                       [Formatted Output]                            │
         │                                                                     │
         └─────────────────────────────────────────────────────────────────────┘

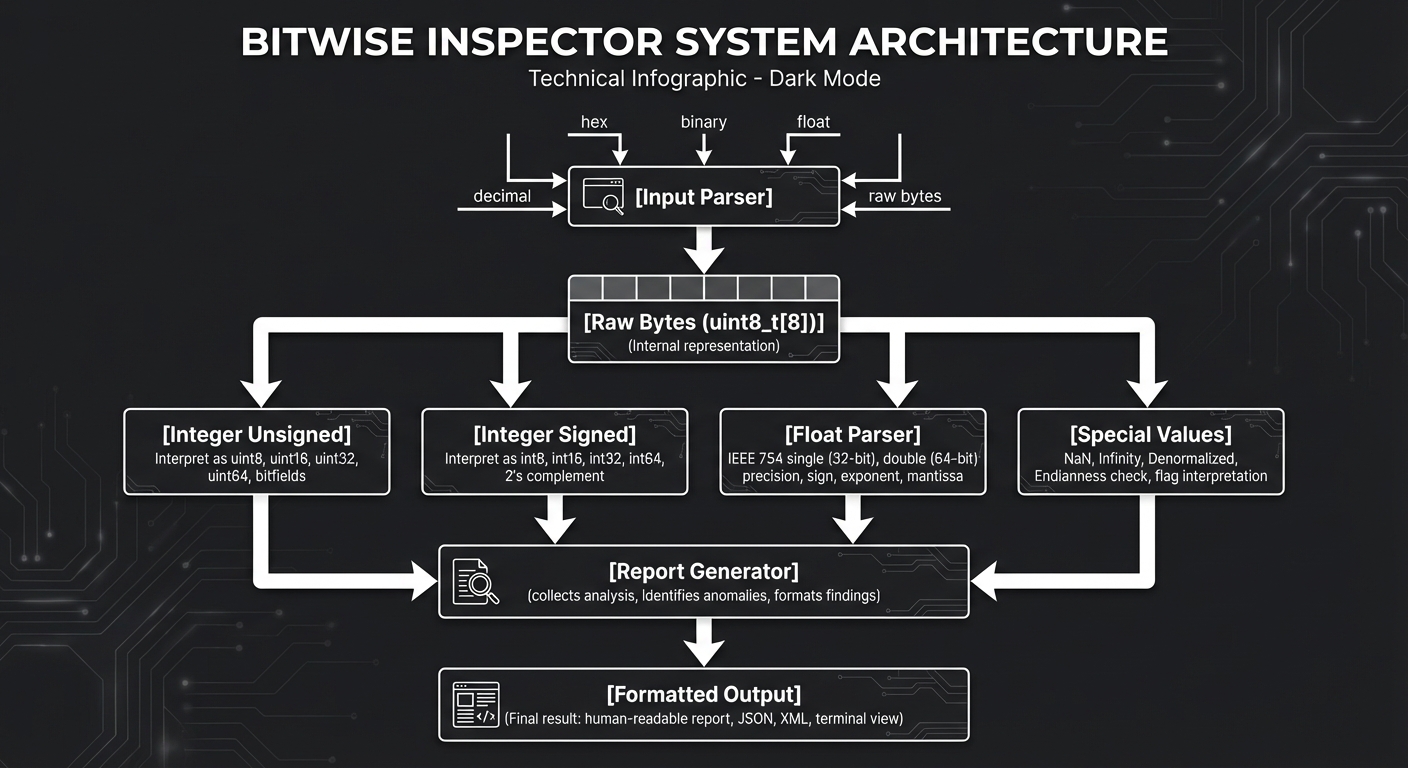
4.2 Module Structure

bitwise-inspector/
├── src/
│   ├── main.c              # Entry point, CLI argument parsing
│   ├── parser.c            # Parse input strings to raw bytes
│   ├── parser.h
│   ├── integer.c           # Integer interpretation and display
│   ├── integer.h
│   ├── floating.c          # IEEE-754 parsing and display
│   ├── floating.h
│   ├── endian.c            # Endianness detection and conversion
│   ├── endian.h
│   ├── display.c           # Formatted output generation
│   ├── display.h
│   └── util.c              # Helper functions
│   └── util.h
├── tests/
│   ├── test_parser.c
│   ├── test_integer.c
│   ├── test_floating.c
│   └── run_tests.sh
├── Makefile
└── README.md

4.3 Key Data Structures

/* Core representation: 8 bytes that can hold any value */
typedef struct {
    uint8_t bytes[8];       /* Raw byte storage */
    size_t num_bytes;       /* How many bytes are meaningful */
    int is_negative;        /* Was input a negative number? */
    int is_float;           /* Was input floating-point? */
    int is_double;          /* Was input double precision? */
} RawValue;

/* Integer interpretation */
typedef struct {
    uint64_t unsigned_val;
    int64_t signed_val;
    size_t width_bits;      /* 8, 16, 32, or 64 */
    int overflows_signed;   /* Would overflow if treated as signed */
} IntegerInterp;

/* IEEE-754 interpretation */
typedef struct {
    int sign;               /* 0 = positive, 1 = negative */
    int exponent_raw;       /* Raw biased exponent */
    int exponent_actual;    /* Actual exponent (unbiased) */
    uint64_t mantissa;      /* Raw mantissa bits */
    double value;           /* Computed floating value */

    /* Classification */
    enum {
        FP_NORMAL,
        FP_DENORMAL,
        FP_ZERO,
        FP_INFINITY,
        FP_NAN_QUIET,
        FP_NAN_SIGNALING
    } category;

    int is_double;          /* 32-bit vs 64-bit */
} FloatInterp;

/* System information */
typedef struct {
    int is_little_endian;
    size_t sizeof_int;
    size_t sizeof_long;
    size_t sizeof_ptr;
    size_t sizeof_float;
    size_t sizeof_double;
} SystemInfo;

4.4 Algorithm Overview

Main Algorithm Flow:

Parse input -> Determine input type and convert to raw bytes
Detect system -> Query endianness and type sizes
Integer interpretations -> For each bit width (8, 16, 32, 64):
- Extract that many bytes
- Interpret as unsigned and signed
- Check for special values (TMin, max values)
Float interpretations -> For float and double:
- Extract sign, exponent, mantissa fields
- Classify (normal, denormal, zero, infinity, NaN)
- Compute actual value
- Note precision issues
Generate report -> Format all interpretations with ASCII diagrams

5. Implementation Guide

5.1 Development Environment Setup

# Required tools
# On macOS
xcode-select --install

# On Linux (Debian/Ubuntu)
sudo apt-get install gcc gdb build-essential

# Create project structure
mkdir -p bitwise-inspector/{src,tests,include}
cd bitwise-inspector

5.2 Implementation Phases

Phase 1: Foundation (Days 1-2)

Goals:

Set up build system
Implement endianness detection
Create basic binary/hex output

Tasks:

Create Makefile: ```makefile CC = gcc CFLAGS = -Wall -Wextra -std=c11 -g SRCDIR = src OBJDIR = obj SOURCES = $(wildcard $(SRCDIR)/*.c) OBJECTS = $(SOURCES:$(SRCDIR)/%.c=$(OBJDIR)/%.o) TARGET = bitwise-inspector

all: $(TARGET)

$(TARGET): $(OBJECTS) $(CC) $(OBJECTS) -o $@

$(OBJDIR)/%.o: $(SRCDIR)/%.c | $(OBJDIR) $(CC) $(CFLAGS) -c $< -o $@

$(OBJDIR): mkdir -p $(OBJDIR)

clean: rm -rf $(OBJDIR) $(TARGET)

2. Implement endianness detection:
```c
/* endian.c */
#include <stdint.h>

int detect_endianness(void) {
    uint32_t x = 0x01020304;
    uint8_t *ptr = (uint8_t *)&x;

    if (ptr[0] == 0x04) return 1;  /* Little-endian */
    if (ptr[0] == 0x01) return 0;  /* Big-endian */
    return -1;  /* Unknown */
}

void print_bytes(const void *ptr, size_t size) {
    const uint8_t *bytes = (const uint8_t *)ptr;
    for (size_t i = 0; i < size; i++) {
        printf("%02X ", bytes[i]);
    }
    printf("\n");
}

Implement binary string conversion:

/* util.c */
void to_binary_string(uint64_t value, int bits, char *out) {
 for (int i = bits - 1; i >= 0; i--) {
     *out++ = (value >> i) & 1 ? '1' : '0';
     if (i > 0 && i % 4 == 0) *out++ = ' ';  /* Nibble separator */
 }
 *out = '\0';
}

Checkpoint: Program prints its own endianness and can show any integer in binary/hex.

Phase 2: Input Parsing (Days 3-4)

Goals:

Parse decimal, hex, binary, and float inputs
Handle negative numbers correctly
Validate input

Tasks:

Implement input type detection: ```c typedef enum { INPUT_DECIMAL, INPUT_HEX, INPUT_BINARY, INPUT_FLOAT, INPUT_BYTES, INPUT_INVALID } InputType;

InputType detect_input_type(const char *input);

2. Parse each type:
```c
int parse_decimal(const char *input, RawValue *out);
int parse_hex(const char *input, RawValue *out);      /* 0x prefix */
int parse_binary(const char *input, RawValue *out);   /* 0b prefix */
int parse_float(const char *input, RawValue *out);
int parse_bytes(const char *input, RawValue *out);    /* "XX XX XX" */

Handle edge cases:
- Leading zeros
- Negative numbers with different bases
- Overflow during parsing
- Scientific notation for floats

Checkpoint: Can parse 42, -1, 0xDEAD, 0b1010, 3.14, 1e-10.

Phase 3: Integer Interpretation (Days 5-7)

Goals:

Show signed/unsigned interpretations at all bit widths
Detect and explain special values
Show sign extension/truncation effects

Tasks:

Implement multi-width interpretation:

void interpret_as_integers(const RawValue *val, IntegerInterp *results) {
 /* Interpret at 8, 16, 32, 64 bit widths */
 uint64_t raw = bytes_to_uint64(val->bytes, val->num_bytes);

 /* 8-bit */
 results[0].width_bits = 8;
 results[0].unsigned_val = raw & 0xFF;
 results[0].signed_val = (int8_t)(raw & 0xFF);

 /* 16-bit */
 results[1].width_bits = 16;
 results[1].unsigned_val = raw & 0xFFFF;
 results[1].signed_val = (int16_t)(raw & 0xFFFF);

 /* ... and so on for 32, 64 */
}

Detect special values:

void check_special_integers(IntegerInterp *interp) {
 if (interp->width_bits == 32) {
     if (interp->signed_val == INT32_MIN)
         interp->is_tmin = 1;
     if (interp->signed_val == INT32_MAX)
         interp->is_tmax = 1;
     if (interp->unsigned_val == UINT32_MAX)
         interp->is_umax = 1;
 }
 /* Similar for other widths */
}

Generate warnings:

void warn_signed_unsigned_difference(const IntegerInterp *interp) {
 /* If MSB is 1, signed and unsigned interpretations differ wildly */
 uint64_t msb_mask = 1ULL << (interp->width_bits - 1);
 if (interp->unsigned_val & msb_mask) {
     printf("  ⚠ WARNING: MSB is set. Signed/unsigned interpretations differ!\n");
 }
}

Checkpoint: Correctly shows that 0xFF is 255 unsigned but -1 signed (8-bit).

Phase 4: Floating-Point Interpretation (Days 8-11)

Goals:

Extract IEEE-754 fields
Classify special values
Compute actual values
Show precision warnings

Tasks:

Extract float fields:

void parse_ieee754_float(uint32_t bits, FloatInterp *out) {
 out->sign = (bits >> 31) & 1;
 out->exponent_raw = (bits >> 23) & 0xFF;
 out->mantissa = bits & 0x7FFFFF;

 /* Classify */
 if (out->exponent_raw == 0) {
     if (out->mantissa == 0)
         out->category = FP_ZERO;
     else
         out->category = FP_DENORMAL;
 } else if (out->exponent_raw == 255) {
     if (out->mantissa == 0)
         out->category = FP_INFINITY;
     else if (out->mantissa & 0x400000)
         out->category = FP_NAN_QUIET;
     else
         out->category = FP_NAN_SIGNALING;
 } else {
     out->category = FP_NORMAL;
 }
}

Compute actual value:

double compute_float_value(const FloatInterp *fp) {
 if (fp->category == FP_INFINITY)
     return fp->sign ? -INFINITY : INFINITY;
 if (fp->category == FP_NAN_QUIET || fp->category == FP_NAN_SIGNALING)
     return NAN;
 if (fp->category == FP_ZERO)
     return fp->sign ? -0.0 : 0.0;

 double mantissa_val;
 int exp_actual;

 if (fp->category == FP_DENORMAL) {
     mantissa_val = fp->mantissa / (double)(1 << 23);  /* 0.mantissa */
     exp_actual = -126;  /* Fixed for denormals */
 } else {
     mantissa_val = 1.0 + fp->mantissa / (double)(1 << 23);  /* 1.mantissa */
     exp_actual = fp->exponent_raw - 127;
 }

 double result = mantissa_val * pow(2, exp_actual);
 return fp->sign ? -result : result;
}

Detect precision issues:

void warn_precision_loss(double original_input, double stored) {
 double diff = fabs(original_input - stored);
 double rel_error = diff / fabs(original_input);

 if (rel_error > 1e-15) {
     printf("  ⚠ PRECISION WARNING: Input cannot be exactly represented!\n");
     printf("     Requested: %.17g\n", original_input);
     printf("     Stored:    %.17g\n", stored);
     printf("     Error:     %.3e\n", diff);
 }
}

Checkpoint: Correctly identifies 0x7F800000 as +Infinity, 0xFFC00000 as NaN.

Phase 5: Display and Polish (Days 12-14)

Goals:

Create formatted ASCII output
Add binary diagrams
Handle edge cases
Add comparison mode

Tasks:

Create field visualization:

void print_float_fields_diagram(const FloatInterp *fp) {
 printf("  Binary breakdown:\n");
 printf("  ┌───┬─────────────────────┬───────────────────────────────────────┐\n");
 printf("  │ S │      Exponent       │               Mantissa                │\n");
 printf("  │ %d │ ", fp->sign);
 print_bits(fp->exponent_raw, 8);
 printf(" │ ");
 print_bits(fp->mantissa, 23);
 printf(" │\n");
 printf("  └───┴─────────────────────┴───────────────────────────────────────┘\n");
}

Add comparison mode:

void compare_values(const char *input1, const char *input2) {
 RawValue v1, v2;
 parse_input(input1, &v1);
 parse_input(input2, &v2);

 printf("Comparing: %s vs %s\n", input1, input2);
 printf("Same bits?     %s\n", memcmp(v1.bytes, v2.bytes, 8) == 0 ? "YES" : "NO");
 printf("Same as int?   %s\n", to_int64(&v1) == to_int64(&v2) ? "YES" : "NO");
 printf("Same as float? %s\n", to_double(&v1) == to_double(&v2) ? "YES" : "NO");
}

Checkpoint: Full formatted output matching specification examples.

6. Testing Strategy

6.1 Test Categories

Category	Purpose	Examples
Boundary Values	Test edge cases	0, -1, MAX, MIN
Type Conversions	Verify cast behavior	-1 as unsigned, float to int
Special Values	Handle IEEE-754 specials	NaN, Infinity, denormals
Precision	Verify accuracy	0.1, 0.3, large floats
Input Parsing	Handle all formats	hex, binary, scientific

6.2 Critical Test Cases

Integer Tests:

/* Two's complement boundaries */
assert(inspect(0).signed_8 == 0);
assert(inspect(127).signed_8 == 127);
assert(inspect(128).signed_8 == -128);
assert(inspect(255).signed_8 == -1);
assert(inspect(-1).unsigned_8 == 255);

/* TMin special case */
assert(inspect(INT32_MIN).hex == "0x80000000");
assert(inspect(-INT32_MIN).value == INT32_MIN);  /* -TMin == TMin! */

/* Overflow detection */
assert(inspect(256).overflows_8bit == 1);

Floating-Point Tests:

/* Special values */
assert(inspect(0x7F800000).float_category == FP_INFINITY);
assert(inspect(0xFF800000).float_category == FP_INFINITY);  /* negative */
assert(inspect(0x7FC00000).float_category == FP_NAN);
assert(inspect(0x00400000).float_category == FP_DENORMAL);
assert(inspect(0x00000000).float_category == FP_ZERO);
assert(inspect(0x80000000).float_category == FP_ZERO);  /* -0.0 */

/* Precision tests */
assert(inspect("0.1").exact_representation == 0);
assert(inspect("0.5").exact_representation == 1);  /* 0.5 is exact! */
assert(inspect("0.25").exact_representation == 1);

/* NaN behavior */
float nan1 = inspect(0x7FC00000).float_value;
assert(nan1 != nan1);  /* NaN != NaN */

Endianness Tests:

/* Same bytes, different interpretations */
uint8_t bytes[] = {0x01, 0x02, 0x03, 0x04};
assert(interpret_le_32(bytes) == 0x04030201);
assert(interpret_be_32(bytes) == 0x01020304);

6.3 Test Data for Edge Cases

/* Integer edge cases */
{"0", "0x00", 0, 0},
{"-1", "0xFF", 255, -1},
{"127", "0x7F", 127, 127},
{"128", "0x80", 128, -128},
{"255", "0xFF", 255, -1},
{"-128", "0x80", 128, -128},
{"2147483647", "0x7FFFFFFF", 2147483647, 2147483647},
{"2147483648", "0x80000000", 2147483648, -2147483648},
{"-2147483648", "0x80000000", 2147483648, -2147483648},

/* Float edge cases */
{"0.0", "0x00000000", "zero"},
{"-0.0", "0x80000000", "negative zero"},
{"inf", "0x7F800000", "positive infinity"},
{"-inf", "0xFF800000", "negative infinity"},
{"nan", "0x7FC00000", "quiet NaN"},

/* Denormals */
{"1.4e-45", "0x00000001", "smallest positive denormal"},
{"1.17e-38", "0x00800000", "smallest positive normal"},

/* Precision edge cases */
{"0.1", "cannot be exactly represented"},
{"0.5", "exactly representable"},
{"16777216", "largest int exactly representable in float"},
{"16777217", "NOT exactly representable in float"},

7. Common Pitfalls & Debugging

7.1 Frequent Mistakes

Pitfall	Symptom	Solution
Wrong printf format	Garbage output for 64-bit values	Use `PRIu64`, `PRIx64` from `<inttypes.h>`
Signed right shift	Unexpected 1s in high bits	Use unsigned types for bit manipulation
Float comparison	NaN comparisons always false	Use `isnan()` from `<math.h>`
Endian confusion	Bytes in wrong order	Be explicit about byte order in code
Integer promotion	Silent widening changes values	Cast explicitly
Denormal handling	Wrong values near zero	Check exponent == 0 case

7.2 Debugging Strategies

Print bytes explicitly:

void debug_print_bytes(const void *ptr, size_t n, const char *label) {
    fprintf(stderr, "[DEBUG] %s: ", label);
    const uint8_t *bytes = ptr;
    for (size_t i = 0; i < n; i++) {
        fprintf(stderr, "%02X ", bytes[i]);
    }
    fprintf(stderr, "\n");
}

Verify with known values:

/* These should always work */
float f = 1.0f;
uint32_t bits;
memcpy(&bits, &f, sizeof(bits));
assert(bits == 0x3F800000);  /* 1.0 has known encoding */

double d = 1.0;
uint64_t dbits;
memcpy(&dbits, &d, sizeof(dbits));
assert(dbits == 0x3FF0000000000000ULL);

Use union for type punning (carefully):

/* Note: technically undefined in C, but widely supported */
union {
    float f;
    uint32_t i;
} u;
u.f = 3.14f;
printf("3.14 as bits: 0x%08X\n", u.i);

/* Preferred approach: memcpy */
float f = 3.14f;
uint32_t bits;
memcpy(&bits, &f, sizeof(bits));  /* Safe and portable */

7.3 Common Calculation Errors

Wrong sign extension:

/* WRONG: sign-extends in 32-bit, then zero-extends to 64-bit */
int8_t x = -1;
uint64_t wrong = (uint64_t)(uint32_t)x;  /* 0x00000000FFFFFFFF */

/* RIGHT: sign-extend directly to 64-bit first */
int8_t x = -1;
uint64_t right = (uint64_t)(int64_t)x;   /* 0xFFFFFFFFFFFFFFFF */

Wrong float field extraction:

/* WRONG: shifts signed value */
int32_t bits = *(int32_t *)&my_float;
int exp = (bits >> 23) & 0xFF;  /* May have sign extension issues */

/* RIGHT: use unsigned */
uint32_t bits;
memcpy(&bits, &my_float, sizeof(bits));
unsigned exp = (bits >> 23) & 0xFF;  /* Always correct */

8. Extensions & Challenges

8.1 Beginner Extensions

Add color output: Highlight special values in red, headers in blue
JSON output mode: --json for machine-readable output
Interactive mode: Loop to inspect multiple values
History: Remember and compare recent inspections

8.2 Intermediate Extensions

Expression evaluation: inspect "0xFF + 1" shows overflow
Type annotation: inspect -t uint32_t 0xDEADBEEF
Struct layout: Show padding for struct definitions
Memory dump mode: Read bytes from file or stdin
x86 instruction bytes: Identify common instruction prefixes

8.3 Advanced Extensions

Arbitrary precision: Handle >64 bit integers (use GMP)
Extended precision: 80-bit x87 floats, 128-bit quad
SIMD visualization: Show __m128, __m256 vector contents
Debugger integration: Plugin for GDB/LLDB
Web interface: WASM-compiled inspector in browser

9. Real-World Connections

9.1 Security Applications

Integer overflow vulnerabilities:

/* Classic vulnerability pattern */
size_t size = user_input;
size_t total = size * sizeof(struct item);  /* Can overflow! */
void *buf = malloc(total);  /* Allocates less than expected */
/* Buffer overflow when filling buf with 'size' items */

Your tool helps identify when values wrap around unexpectedly.

Floating-point comparison bugs:

/* Dangerous financial code */
if (balance - withdrawal == 0.0) {  /* May fail due to precision! */
    close_account();
}

9.2 Systems Programming

Network byte order:

/* Data from network is big-endian */
uint32_t net_value;
recv(sock, &net_value, 4, 0);
uint32_t host_value = ntohl(net_value);  /* Convert to host order */

Your tool shows exactly how byte ordering affects interpretation.

Binary file formats:

ELF header starts with:
7F 45 4C 46  →  ".ELF" magic number
02           →  64-bit
01           →  little-endian

Understanding byte-level representation is essential for parsing binary formats.

9.3 Embedded Systems

Fixed-point arithmetic:

/* When floats are too slow, use fixed-point */
typedef int32_t fixed_16_16;  /* 16 bits integer, 16 bits fraction */

fixed_16_16 a = 0x00018000;  /* 1.5 */
fixed_16_16 b = 0x00020000;  /* 2.0 */
fixed_16_16 c = (a * b) >> 16;  /* Multiply and shift */

9.4 Scientific Computing

Precision loss in accumulation:

float sum = 0.0f;
for (int i = 0; i < 1000000; i++) {
    sum += 0.1f;  /* Each addition loses precision */
}
/* sum is NOT 100000.0! Probably around 100958.xxx */

Catastrophic cancellation:

float a = 1.00000001f;
float b = 1.00000000f;
float diff = a - b;  /* Nearly all significant digits lost! */

10. Resources

10.1 Essential Reading

From Your Collection:

CS:APP Chapter 2: “Representing and Manipulating Information” - The definitive treatment
CS:APP Chapter 3: “Machine-Level Representation of Programs” - Data sizes and alignment
Effective C, 2nd Edition: Chapter on integers and type conversions

Additional:

“What Every Computer Scientist Should Know About Floating-Point Arithmetic” by David Goldberg - Essential float understanding
IEEE 754-2019 Standard - Official floating-point specification

10.2 Online Tools for Verification

IEEE-754 Floating Point Converter: https://www.h-schmidt.net/FloatConverter/IEEE754.html
Two’s Complement Calculator: Various online tools
Compiler Explorer (godbolt.org): See how C code becomes assembly

Previous: P1 (Toolchain Explorer) - Understanding how data gets into binaries
Next: P3 (Data Lab Clone) - Bit manipulation puzzles using these concepts
Related: P4 (Calling Convention) - How data is passed at machine level

10.4 Video Resources

CS:APP Video Lectures: CMU’s own lectures covering Chapter 2
Ben Eater’s videos: Low-level computer concepts explained visually

11. Self-Assessment Checklist

Understanding Verification

Two’s Complement:

I can convert any 8-bit value between signed and unsigned interpretations mentally
I can explain why -(-128) == -128 in 8-bit signed arithmetic
I know the range of signed and unsigned for any bit width
I understand why signed overflow is undefined behavior in C

IEEE-754:

I can identify the three fields in a float/double
I understand why the leading 1 is implicit in normalized numbers
I can recognize NaN, Infinity, and denormal patterns
I can explain why 0.1 + 0.2 != 0.3

Endianness:

I know which byte order my machine uses
I can convert between big-endian and little-endian interpretations
I understand when byte order matters (multi-byte values) and when it doesn’t (single bytes)

Implementation Verification

Tool correctly parses decimal, hex, binary, and float inputs
All integer interpretations (8, 16, 32, 64-bit, signed/unsigned) are correct
IEEE-754 field extraction is correct for both float and double
Special values (NaN, Infinity, denormals) are correctly identified
Endianness is correctly detected and displayed
Output format is clear and educational

Growth Verification

I fixed at least one bug by examining raw byte patterns
I can predict the output of my tool for new inputs before running it
I understand common patterns that cause bugs (signed/unsigned comparison, precision loss)
I can explain bit-level representation to someone else

12. Submission / Completion Criteria

Minimum Viable Completion:

Parses integer inputs (decimal and hex)
Shows byte representation
Shows signed/unsigned interpretations for 32-bit
Detects system endianness

Full Completion:

All input formats work (decimal, hex, binary, float, bytes)
All bit widths shown (8, 16, 32, 64)
IEEE-754 interpretation with field breakdown
Special value detection and explanation
Clean formatted output with ASCII diagrams
Test suite with edge cases

Excellence (Going Above & Beyond):

Expression evaluation
Comparison mode between values
Interactive REPL mode
Color terminal output
Web or GUI interface

13. Real World Outcome

When you complete this project, here’s exactly what you’ll see when running your tool:

$ ./bitwise-inspector -128

===============================================================================
                          BITWISE DATA INSPECTOR
                              Input: -128
===============================================================================

BYTE REPRESENTATION (little-endian system)
--------------------------------------------------------------------------------
  Memory order:    80 FF FF FF FF FF FF FF
  Logical order:   FF FF FF FF FF FF FF 80

BINARY VIEW (64-bit)
--------------------------------------------------------------------------------
  1111 1111 1111 1111 1111 1111 1111 1111
  1111 1111 1111 1111 1111 1111 1000 0000
  ^                                  ^
  |                                  +-- Lowest 7 bits = 0
  +-- Sign bit = 1 (negative in two's complement)

  Binary breakdown:
    Position 7: 1 x -128 = -128
    Position 6: 0 x   64 =    0
    Position 5: 0 x   32 =    0
    Position 4: 0 x   16 =    0
    Position 3: 0 x    8 =    0
    Position 2: 0 x    4 =    0
    Position 1: 0 x    2 =    0
    Position 0: 0 x    1 =    0
                          ------
    8-bit signed total:    -128  (TMin for 8-bit!)

INTEGER INTERPRETATIONS
--------------------------------------------------------------------------------
  Type             Hex                      Decimal
  ----             ---                      -------
  uint8_t          0x80                     128
  int8_t           0x80                     -128  <-- TMin (no positive equivalent!)
  uint16_t         0xFF80                   65408
  int16_t          0xFF80                   -128
  uint32_t         0xFFFFFF80               4294967168
  int32_t          0xFFFFFF80               -128
  uint64_t         0xFFFFFFFFFFFFFF80       18446744073709551488
  int64_t          0xFFFFFFFFFFFFFF80       -128

  SIGN EXTENSION ANALYSIS:
    Original 8-bit value: 0x80 (-128)
    Extended to 16-bit:   0xFF80 (sign bit copied to upper 8 bits)
    Extended to 32-bit:   0xFFFFFF80 (sign bit copied to upper 24 bits)
    Extended to 64-bit:   0xFFFFFFFFFFFFFF80 (sign bit copied to upper 56 bits)

  [!] SPECIAL VALUE: This is TMin (most negative value) for 8-bit signed!
      -(-128) = -128 in 8-bit arithmetic (negation wraps around)

FLOATING-POINT INTERPRETATION
--------------------------------------------------------------------------------
  As float (32-bit):   Hex: 0xFFFFFF80
    Sign:     1 (negative)
    Exponent: 11111111 (255) --> SPECIAL VALUE
    Mantissa: 11111111111111110000000 (non-zero)
    Result:   NaN (quiet) - Not a Number

  As double (64-bit):  Hex: 0xFFFFFFFFFFFFFF80
    Sign:     1 (negative)
    Exponent: 11111111111 (2047) --> SPECIAL VALUE
    Mantissa: 11111111111111111111...0000000 (non-zero)
    Result:   NaN (quiet) - Not a Number

SYSTEM INFO
--------------------------------------------------------------------------------
  Architecture:   x86_64 (little-endian)
  sizeof(int):    4 bytes
  sizeof(long):   8 bytes
  sizeof(float):  4 bytes
  sizeof(double): 8 bytes

===============================================================================


$ ./bitwise-inspector 0.1

===============================================================================
                          BITWISE DATA INSPECTOR
                              Input: 0.1 (floating-point)
===============================================================================

AS DOUBLE (64-bit IEEE-754)
--------------------------------------------------------------------------------
  Hex: 0x3FB999999999999A

  Field Breakdown:
  +---+---------------------+----------------------------------------------------+
  | S |      Exponent       |                    Mantissa                        |
  | 0 | 0 1 1 1 1 1 1 1 0 1 1| 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0|
  +---+---------------------+----------------------------------------------------+
    |          |                              |
    |          |                              +-- Repeating pattern: 1001 1001 1001...
    |          +-- Biased exponent: 1019
    +-- Sign: positive                          Actual exponent: 1019 - 1023 = -4

  Calculation:
    Value = (-1)^0 x 1.1001100110011001100110011001100110011001100110011010 x 2^(-4)
    Value = 1.6 x 0.0625
    Value = 0.10000000000000000555111512312578270211815834045410156250

  [!] PRECISION WARNING:
      Input:       0.1 (exact decimal)
      Stored as:   0.10000000000000000555111512312578...
      Error:       +5.55e-18 (about 1 part in 10^17)

      Why? 0.1 in binary is:
        0.1 (decimal) = 0.0001100110011001100110011... (binary, repeating!)
      Just like 1/3 = 0.333... in decimal, 1/10 cannot be exactly represented in binary.

AS FLOAT (32-bit IEEE-754)
--------------------------------------------------------------------------------
  Hex: 0x3DCCCCCD

  Field Breakdown:
  +---+-------------+-------------------------------+
  | S |  Exponent   |           Mantissa            |
  | 0 | 0 1 1 1 1 0 1 1| 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1|
  +---+-------------+-------------------------------+

  Stored value: 0.10000000149011611938476562500000

  [!] Float has only 23 mantissa bits (vs 52 for double)
      Additional precision loss when converting double to float!

COMPARISON: Why 0.1 + 0.2 != 0.3
--------------------------------------------------------------------------------
  0.1 as double: 0x3FB999999999999A
  0.2 as double: 0x3FC999999999999A
  Sum:           0x3FD3333333333334
  0.3 as double: 0x3FD3333333333333

  0.1 + 0.2 = 0.30000000000000004 (not exactly 0.3!)

===============================================================================

14. The Core Question You’re Answering

“When I write int x = -1 or float y = 0.1, what EXACTLY is stored in memory, and why does that sometimes cause surprising behavior?”

This project transforms the mystery of “the computer just stores numbers somehow” into a complete understanding of two’s complement integers, IEEE-754 floating point, and endianness. You’ll never again be surprised by signed/unsigned comparison bugs or floating-point precision issues.

15. Concepts You Must Understand First

Before starting this project, ensure you understand these concepts:

Concept	Why It Matters	Where to Learn
Binary number system	Everything builds on this	CS:APP 2.1, any discrete math
Hexadecimal notation	Compact representation of bytes	CS:APP 2.1.3
What a “byte” is	Fundamental unit of storage	CS:APP 2.1.1
Pointers in C	You’ll cast pointers to examine bytes	Any C book, Ch. on pointers
printf format specifiers	For displaying values in different formats	C reference manual
Basic understanding of negative numbers in math	Context for two’s complement	High school math

16. Questions to Guide Your Design

Work through these questions BEFORE writing code:

Type Punning: How do you safely view the bytes of a float? (Hint: memcpy is safer than pointer casting)
Endianness Detection: How can your program determine if it’s running on a big-endian or little-endian system?
Input Parsing: How will you distinguish between 42 (integer), 0x2A (hex), 0b101010 (binary), and 42.0 (float)?
Width Handling: If the user enters 300, should you show 8-bit interpretation (which overflows) or just skip it?
Float Field Extraction: How do you extract sign, exponent, and mantissa from a float? What bit masks do you need?
Special Value Detection: How do you detect NaN, Infinity, denormals, and negative zero?
Precision Display: How many decimal places should you show for floating-point values to be accurate but not misleading?

17. Thinking Exercise

Before writing any code, work through this by hand:

Exercise 1: Two’s Complement

For 8-bit signed integers, fill in this table:

Binary	Unsigned	Signed
0000 0000	?	?
0000 0001	?	?
0111 1111	?	?
1000 0000	?	?
1111 1111	?	?
1000 0001	?	?

Now verify: What is -5 in 8-bit binary? Hint: negate 5 (flip bits, add 1).

Exercise 2: IEEE-754 Encoding

Encode the number 5.75 as a 32-bit float:

Convert 5.75 to binary: 5 = 101, 0.75 = 0.11, so 5.75 = 101.11
Normalize: 101.11 = 1.0111 x 2^2
Calculate biased exponent: 2 + 127 = 129 = 10000001
Mantissa (drop the leading 1): 01110000000000000000000
Sign: 0 (positive)

Final: 0 10000001 01110000000000000000000 = 0x40B80000

Verify using your completed tool or an online calculator.

Exercise 3: Why 0.1 + 0.2 != 0.3

What is 0.1 in binary? (Hint: it’s repeating, like 1/3 in decimal)
What happens when you truncate a repeating binary fraction?
When you add two truncated values, is the error additive?

18. The Interview Questions They’ll Ask

After completing this project, you’ll be ready for these common interview questions:

“What is two’s complement and why is it used?”
- Expected: Negation by flipping bits and adding 1; hardware can use the same circuits for signed/unsigned addition
- Bonus: Explain why there’s one more negative number than positive (TMin has no positive counterpart)
“What happens when you cast a negative int to unsigned?”
- Expected: Bit pattern stays the same, interpretation changes; -1 becomes UINT_MAX
- Bonus: Explain why this causes bugs in comparisons like if (signed_val < unsigned_val)
“Why is 0.1 + 0.2 not equal to 0.3 in floating point?”
- Expected: 0.1 cannot be exactly represented in binary; accumulated rounding error
- Bonus: Explain the mantissa pattern that shows why (repeating 1001)
“What is NaN and how do you check for it?”
- Expected: “Not a Number” from invalid operations like 0/0; NaN != NaN is true
- Bonus: Explain quiet vs signaling NaN, and the bit pattern (exponent all 1s, mantissa non-zero)
“What’s the difference between big-endian and little-endian?”
- Expected: Byte order for multi-byte values; little-endian stores LSB first
- Bonus: Know which architectures use which (x86 is little, network byte order is big)
“What is integer overflow and why is signed overflow undefined behavior in C?”
- Expected: Result wraps around; undefined because different hardware handles it differently
- Bonus: Explain how compilers exploit UB for optimization (can assume no overflow happened)

19. Hints in Layers

If you’re stuck, reveal hints one at a time:

Hint 1: Examining Bytes Safely

Don’t use pointer casting like *(uint32_t*)&f - it’s technically undefined behavior. Use memcpy instead:

float f = 3.14;
uint32_t bits;
memcpy(&bits, &f, sizeof(bits));  // Safe, portable

This is what the C standard guarantees will work.

Hint 2: Extracting Float Fields

For a 32-bit float:

uint32_t bits;
memcpy(&bits, &my_float, sizeof(bits));

int sign = (bits >> 31) & 1;
int exponent = (bits >> 23) & 0xFF;
uint32_t mantissa = bits & 0x7FFFFF;

For doubles, it’s 1 sign bit, 11 exponent bits, 52 mantissa bits.

Hint 3: Detecting Special Values

// For float (32-bit)
if (exponent == 0 && mantissa == 0) → Zero (check sign for +0 vs -0)
if (exponent == 0 && mantissa != 0) → Denormalized
if (exponent == 255 && mantissa == 0) → Infinity
if (exponent == 255 && mantissa != 0) → NaN

The standard library also provides isnan(), isinf(), fpclassify() in <math.h>.

Hint 4: Endianness Detection

int is_little_endian(void) {
    uint32_t x = 1;
    return *(uint8_t*)&x == 1;
}

On little-endian: the 1 is stored in the first byte. On big-endian: the 1 is stored in the last byte.

20. Books That Will Help

Topic	Book	Chapter/Section
Unsigned integers	CS:APP 3rd Ed	Section 2.1.1-2.1.3 “Integral Data Types”
Two’s complement	CS:APP 3rd Ed	Section 2.2 “Two’s-Complement Encodings”
Integer conversions	CS:APP 3rd Ed	Section 2.2.4-2.2.6 “Conversions between Signed and Unsigned”
Integer overflow	CS:APP 3rd Ed	Section 2.3 “Integer Arithmetic”
IEEE-754 floats	CS:APP 3rd Ed	Section 2.4 “Floating Point”
Special float values	CS:APP 3rd Ed	Section 2.4.2 “IEEE Floating-Point Representation”
Floating-point operations	CS:APP 3rd Ed	Section 2.4.4-2.4.5 “Rounding”, “Floating-Point Operations”
Byte ordering	CS:APP 3rd Ed	Section 2.1.4 “Addressing and Byte Ordering”
The classic float paper	“What Every Computer Scientist Should Know About Floating-Point Arithmetic”	David Goldberg, 1991
C type system	Effective C, 2nd Edition	Chapter 3 “Arithmetic Types”

This guide was expanded from CSAPP_3E_DEEP_LEARNING_PROJECTS.md. For the complete learning path, see the project index.

Project 2: Bitwise Data Inspector

Quick Reference

Table of Contents

1. Learning Objectives

2. Deep Theoretical Foundation

2.1 Why Binary Matters

2.2 Unsigned Integers

2.3 Signed Integers: Two’s Complement

2.4 Sign Extension and Truncation

2.5 Signed vs Unsigned Comparisons

2.6 IEEE-754 Floating-Point Representation

2.7 Special Floating-Point Values

2.8 Floating-Point Precision and Rounding

2.9 Endianness

2.10 Data Alignment and Padding

3. Project Specification

3.1 What You Will Build

3.2 Functional Requirements

3.3 Example Usage and Output

4. Solution Architecture

4.1 High-Level Design

4.2 Module Structure

4.3 Key Data Structures

4.4 Algorithm Overview

5. Implementation Guide

5.1 Development Environment Setup

5.2 Implementation Phases

Phase 1: Foundation (Days 1-2)

Phase 2: Input Parsing (Days 3-4)

Phase 3: Integer Interpretation (Days 5-7)

Phase 4: Floating-Point Interpretation (Days 8-11)

Phase 5: Display and Polish (Days 12-14)

6. Testing Strategy

6.1 Test Categories

6.2 Critical Test Cases

6.3 Test Data for Edge Cases

7. Common Pitfalls & Debugging

7.1 Frequent Mistakes

7.2 Debugging Strategies

7.3 Common Calculation Errors

8. Extensions & Challenges

8.1 Beginner Extensions

8.2 Intermediate Extensions

8.3 Advanced Extensions

9. Real-World Connections

9.1 Security Applications

9.2 Systems Programming

9.3 Embedded Systems

9.4 Scientific Computing

10. Resources

10.1 Essential Reading

10.2 Online Tools for Verification

10.3 Related Projects

10.4 Video Resources

11. Self-Assessment Checklist

Understanding Verification

Implementation Verification

Growth Verification

12. Submission / Completion Criteria

13. Real World Outcome

14. The Core Question You’re Answering

15. Concepts You Must Understand First

16. Questions to Guide Your Design

17. Thinking Exercise

18. The Interview Questions They’ll Ask

19. Hints in Layers

20. Books That Will Help